如图，AD为△ABC的中线，BE为△ABD的中线。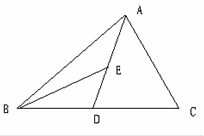
（1）∠ABE=15°，∠BAD=40°，求∠BED的度数；（2）在△BED中作BD边上的高；
（3）若△ABC的面积为40，BD=5，则△BDE 中BD边上的高为多少？
（本小题满分6分）为了进一步了解义务教育阶段学生的体质健康状况，教育部对我市某中学九年级的部分学生进行了体质揣测．体质揣测的结果分为四个等级：优秀、良好、合格、不合格；根据调查结果绘制了下列两幅不完整的统计图，请你根据统计图提供的信息回答以下问题：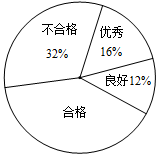
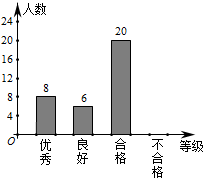
（1）在扇形统计图中，“合格“的百分比为．
（2）本次体质抽测中，抽测结果为“不合格“等级的学生有人．
（3）若该校九年级有400名学生，估计该校九年级体质为“不合格“等级的学生约有人．
（本小题满分6分）先化简，再求值．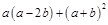
，其中
，
．
已知四边形ABCD内接于⊙O，∠ADC＝90°，∠DCB＜90°，对角线AC平分∠DCB ，延长DA，CB相交于点E．
（1）如图1，EB＝AD，求证：△ABE是等腰直角三角形；
（2）如图2，连接OE，过点E作直线EF，使得∠OEF＝30°，当∠ACE≥30°时，判断直线EF与⊙O的位置关系，并说明理由．
已知点A（－2，n）在抛物线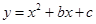
上．
（1）若b＝1，c＝3，求n的值；
（2）若此抛物线经过点B（4，n），且二次函数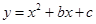的最小值是－4，请画出点P（
，
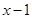）的纵坐标随横坐标变化的图象，并说明理由．
如图，在平面直角坐标系中，点
，
，点
，
在直线
上．四边形
的对角线
，
相交于点
，且
，
，
，
的面积是2．求证：四边形
是矩形．