(本小题满分6分)学生每天体育锻炼不少于1小时的要求,为确保时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:
频数分布表 频数分布直方图
| 时间分组(小时) |
频数(人数) |
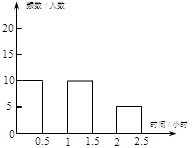 频率 频率 |
 ﹤0.5 ﹤0.5 |
10 |
0.2 |
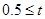 ﹤1 ﹤1 |
|
0.4 |
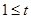 ﹤1.5 ﹤1.5 |
10 |
0.2 |
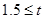 ﹤2 ﹤2 |
|
0.1 |
 ﹤2.5 ﹤2.5 |
5 |
|
| 合 计 |
|
1 |
请你将频数分布表和频数分布直方图补充完整.
如图,折叠矩形ABCD的一边AD使点D落在BC边上的E处,已知折痕AF=10cm,且tan∠FEC=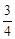 .
.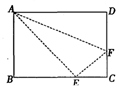
(1)求矩形ABCD的面积;
(2)利用尺规作图求作与四边形AEFD各边都相切的⊙O的圆心O(只须保留作图痕迹),并求出⊙O的半径.
已知关于x的一元二次方程x2-2 x+m=0有两个不相等的实数根.
x+m=0有两个不相等的实数根.
(1)求实数m的最大整数值;
(2)在(1)的条件下,方程的实数根是x1,x2(x1>x2),求代数式x1+2x2的值.
在一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4.随机地摸取一个小球后放回,再随机地摸出一个小球,请用列举法(画树状图或列表)求下列事件的概率:
(1)两次取得小球的标号相同;
(2)两次取得小球的标号的和等于4.
如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,AF是⊙O的弦,且AF⊥BC于D点.求证:(1)△ADC∽△ABE; (2)BE=CF.
已知二次函数y=ax2+bx+1的图像经过(1,2),(2,4)两点.
(1)求a、b值;(2)试判断该函数图像与x轴的交点情况,并说明理由.