已知集合A={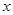 |
|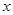 ≤
≤ +3},B={
+3},B={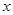 |
|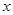 <-1或
<-1或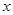 >5}.
>5}.
(1) 若 ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围.
(本大题满分14分)某中学高一年级有x个学生,高二年级有900个学生,高三年级有y个学生,采用分层抽样法抽取一个容量为370人的样本,其中从高一年级抽取120人,高三年级抽取100人,则全校高中部共有多少学生?
( 本小题满分14)
某次考试,满分100分,按规定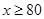 者为良好,
者为良好,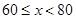 者为及格,小于60者不及格,画出当输入一个同学的成绩
者为及格,小于60者不及格,画出当输入一个同学的成绩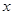 时,输出这个同学属于良好、及格还是不及格的程序框图.
时,输出这个同学属于良好、及格还是不及格的程序框图.
( 本小题满分14)
已知点A(-4,-5),B(6,-1),求以线段AB为直径的圆的方程。
( 本小题满分14)
如图,在三棱锥P—ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.
(1)求证:DE∥平面PAC
(2)求证:AB⊥PB
( 本小题满分12)
已知直线l经过点(0,-2),其斜率是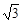 .
.
(1)求直线l的方程;
(2)求直线l与两坐标轴围成三角形的面积.