(本大题满分14分)某中学高一年级有x个学生,高二年级有900个学生,高三年级有y个学生,采用分层抽样法抽取一个容量为370人的样本,其中从高一年级抽取120人,高三年级抽取100人,则全校高中部共有多少学生?
已知函数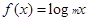 (
(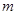 为常数,
为常数,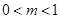 ),且数列
),且数列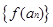 是首项为
是首项为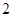 ,公差为
,公差为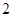 的等差数列.
的等差数列.
(1) 若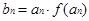 ,当
,当 时,求数列
时,求数列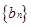 的前
的前 项和
项和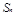 ;
;
(2)设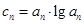 ,如果
,如果 中的每一项恒小于它后面的项,求
中的每一项恒小于它后面的项,求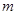 的取值范围.
的取值范围.
已知中心在原点 ,焦点在x轴上,离心率为
,焦点在x轴上,离心率为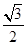 的椭圆过点(
的椭圆过点( ,
, ).
).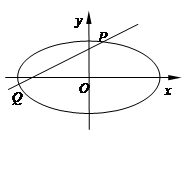
(1)求椭圆的方程;
(2)设不过原点 的直线与该椭圆交于
的直线与该椭圆交于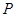 、
、 两点,满足直线
两点,满足直线 ,
,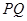 ,
,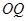 的斜率依次成等比数列,求
的斜率依次成等比数列,求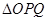 面积的取值范围.
面积的取值范围.
如图,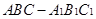 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
,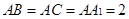 ,点
,点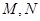 分别为
分别为 和
和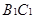 的中点.
的中点.
(1)证明: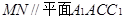 ;
;
(2)求二面角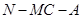 的正弦值.
的正弦值.
在某校高三学生的数学校本课程选课过程中,规定每位同学只能选一个科目。已知某班第一小组与第二小组各 有六位同学选择科目甲或科 目乙,情况如下表:
| 科目甲 |
科目乙 |
总计 |
|
| 第一小组 |
1 |
5 |
6 |
| 第二小组 |
2 |
4 |
6 |
| 总计 |
3 |
9 |
12 |
现从第一小组、第二小 组中各任选2人分析选课情况.
(1)求选出的4 人均选科目乙的概率;
(2)设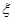 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求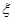 的分布列和数学期望.
的分布列和数学期望.
已知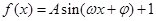 ,(
,(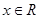 ,其中
,其中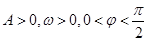 )的周期为
)的周期为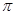 ,且图像上一个最低点为
,且图像上一个最低点为
(1)求 的解析式;
的解析式;
(2)当 时,求
时,求 的值域.
的值域.