已知中心在原点 ,焦点在x轴上,离心率为
,焦点在x轴上,离心率为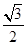 的椭圆过点(
的椭圆过点( ,
, ).
).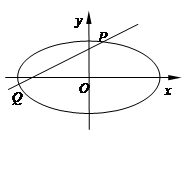
(1)求椭圆的方程;
(2)设不过原点 的直线与该椭圆交于
的直线与该椭圆交于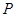 、
、 两点,满足直线
两点,满足直线 ,
,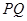 ,
,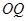 的斜率依次成等比数列,求
的斜率依次成等比数列,求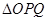 面积的取值范围.
面积的取值范围.
(1 2分)判断函数y=
2分)判断函数y=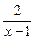 在区间[2,6]上的单调性,并求最大值和最小值.
在区间[2,6]上的单调性,并求最大值和最小值.
(10分)解不等式 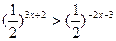
(14分)已知圆M过定点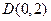 ,圆心M在二次曲线
,圆心M在二次曲线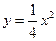 上运动(1)若圆M与y轴相切,求圆M方程;(2) 已知圆M的圆心M在第一象限, 半径为
上运动(1)若圆M与y轴相切,求圆M方程;(2) 已知圆M的圆心M在第一象限, 半径为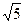 ,动点
,动点 是圆M外一点,过点
是圆M外一点,过点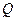 与圆M相切的切线的长为3,求动点
与圆M相切的切线的长为3,求动点 的轨迹方程;(3)若圆M与x轴交于A,B两点,设
的轨迹方程;(3)若圆M与x轴交于A,B两点,设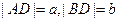 ,求
,求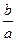 的取值范围?
的取值范围?
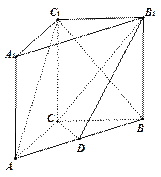
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到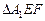 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求二面角A1-BP-E的大小。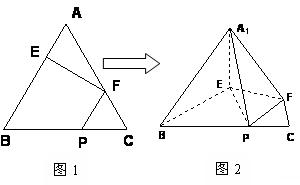
已知三棱柱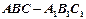 的三视图如图所示,
的三视图如图所示, 其中正视图
其中正视图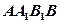 和侧视图
和侧视图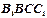 均为矩形,俯视图
均为矩形,俯视图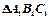 中,
中,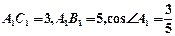 。
。
(I)在三棱柱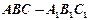 中,求证:
中,求证: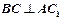 ;
;
(II)在三棱柱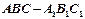 中,若
中,若 是底边
是底边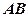 的中点,求证:
的中点,求证: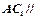 平面
平面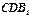 ;
;