(本小题满分8分)按右图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(a)新数据都在60~100(含60和100)之间;
(b)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。
(1)若y与x的关系是y=x+p(100-x),请说明:当p=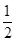 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;
(2)若按关系式y=a(x-h)2+k (a>0)将数据进行变换,请写出一个满足上述要求的这种关系式。(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)
阅读下列材料并回答问题:
材料1:如果一个三角形的三边长分别为 , , ,记 ,那么三角形的面积为 . ①
古希腊几何学家海伦 ,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约 约 ,曾提出利用三角形的三边求面积的秦九韶公式: . ②
下面我们对公式②进行变形: .
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦 秦九韶公式.
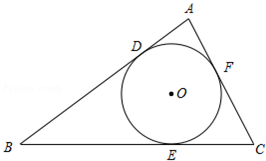
问题:如图,在 中, , , , 内切于 ,切点分别是 、 、 .
(1)求 的面积;
(2)求 的半径.
在创建“全国文明城市”和“省级文明城区”过程中,栾城区污水处理厂决定先购买 、 两型污水处理设备共20台,对城区周边污水进行处理.已知每台 型设备价格为12万元,每台 型设备价格为10万元;1台 型设备和2台 型设备每周可以处理污水640吨,2台 型设备和3台 型设备每周可以处理污水1080吨.
(1)求 、 两型污水处理设备每周分别可以处理污水多少吨?
(2)要想使污水处理厂购买设备的资金不超过230万元,但每周处理污水的量又不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
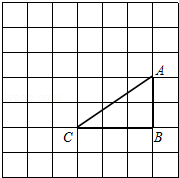
如图,在边长为1的正方形网格中, 的顶点均在格点上,点 、 的坐标分别是 、 ,把 绕点 逆时针旋转 后得到△ .
(1)画出△ ,直接写出点 、 的坐标;
(2)求在旋转过程中, 所扫过的面积.
为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,以便国家精准扶贫政策有效落实.统计发现班上贫困家庭学生人数分别有2名、3名、4名、5名、6名,共五种情况.并将其制成了如下两幅不完整的统计图:
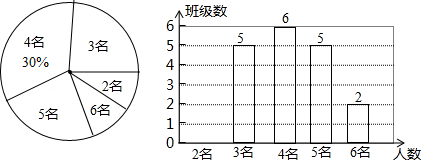
(1)求该校一共有多少个班?并将条形图补充完整;
(2)某爱心人士决定从2名贫困家庭学生的这些班级中,任选两名进行帮扶,请用列表法或树状图的方法,求出被选中的两名学生来自同一班级的概率.
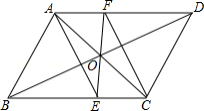
如图, 的对角线 、 交于点 , 过点 且与 、 分别交于点 、 .试猜想线段 、 的关系,并说明理由.