已知x,y为正实数,满足1≤lg(xy)≤2,3≤lg ≤4,求lg(x4y2)的取值范围.
≤4,求lg(x4y2)的取值范围.
已知双曲线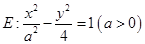 的中心为原点
的中心为原点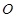 ,左、右焦点分别为
,左、右焦点分别为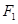 、
、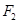 ,离心率为
,离心率为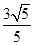 ,点
,点 是直线
是直线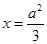 上任意一点,点
上任意一点,点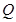 在双曲线
在双曲线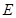 上,且满足
上,且满足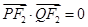 .
.
(1)求实数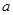 的值;
的值;
(2)证明:直线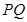 与直线
与直线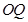 的斜率之积是定值;
的斜率之积是定值;
(3)若点 的纵坐标为
的纵坐标为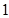 ,过点
,过点 作动直线
作动直线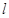 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点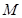 、
、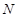 ,在线段
,在线段 上去异于点
上去异于点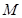 、
、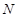 的点
的点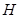 ,满足
,满足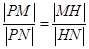 ,证明点
,证明点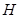 恒在一条定直线上.
恒在一条定直线上.
已知函数 .
.
(1)求函数 的极值;
的极值;
(2)定义:若函数 在区间
在区间 上的取值范围为
上的取值范围为 ,则称区间
,则称区间 为函数
为函数 的“域同区间”.试问函数
的“域同区间”.试问函数 在
在 上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
已知等差数列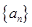 的首项为
的首项为 ,公差为
,公差为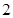 ,数列
,数列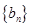 满足
满足 ,
, .
.
(1)求数列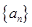 与
与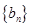 的通项公式;
的通项公式;
(2)记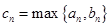 ,求数列
,求数列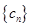 的前
的前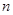 项和
项和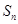 .
.
(注: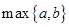 表示
表示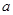 与
与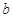 的最大值.)
的最大值.)
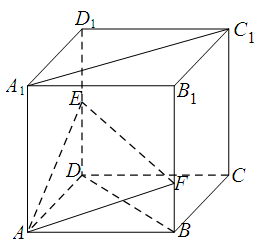
如图,在棱长为 的正方体
的正方体 中,点
中,点 是棱
是棱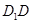 的中点,点
的中点,点 在棱
在棱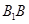 上,且满足
上,且满足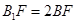 .
.
(1)求证: ;
;
(2)在棱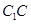 上确定一点
上确定一点 ,使
,使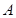 、
、 、
、 、
、 四点共面,并求此时
四点共面,并求此时 的长;
的长;
(3)求几何体 的体积.
的体积.