设函数
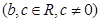 ,且
,且 为
为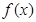 的极值点.
的极值点.
(Ⅰ) 若 为
为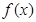 的极大值点,求
的极大值点,求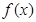 的单调区间(用
的单调区间(用 表示);
表示);
(Ⅱ)若 恰有1解,求实数
恰有1解,求实数 的取值范围.
的取值范围.
如图,直三棱柱 , , 点 分别为 和 的中点。
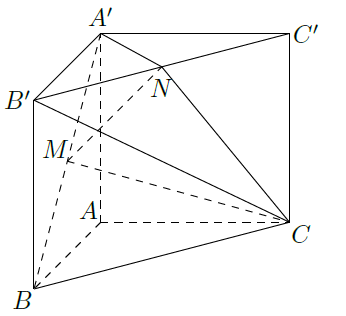
(Ⅰ)证明:
∥平面
;
(Ⅱ)若二面角
为直二面角,求
的值。
在
中,角
、
、
的对边分别为
,
,
角
,
,
成等差数列。
(Ⅰ)求
的值;
(Ⅱ)边
,
,
成等比数列,求
的值。
已知 ,不等式 的解集为
(Ⅰ)求
的值;
(Ⅱ)若
恒成立,求
的取值范围.
在直角坐标
中,圆
,圆
.
(Ⅰ)在以
为极点,
轴正半轴为极轴的极坐标系中,分别写出圆
的极坐标方程,并求出圆
的交点坐标(用极坐标表示);
(Ⅱ)求圆
的公共弦的参数方程.
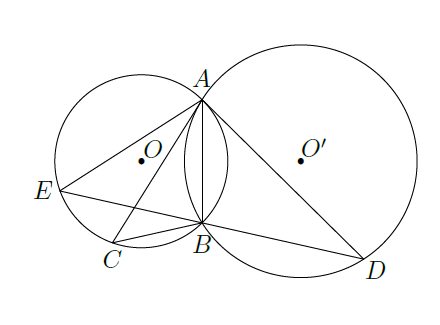
如图,圆
和圆
相交于
两点,过
作两圆的切线分别交两圆于
两点,连接
并延长交圆
于点
。证明:
(Ⅰ)
;
(Ⅱ)
。