某品牌专卖店准备在国庆期间举行促销活动，根据市场调查，该店决定从2种不同型号的洗衣机，2种不同型号的电视机和3种不同型号的空调中（不同种商品的型号不同），选出4种不同型号的商品进行促销，该店对选出的商品采用的促销方案是有奖销售，即在该商品现价的基础上将价格提高150元，同时，若顾客购买任何一种型号的商品，则允许有3次抽奖的机会，若中奖，则每次中奖都获得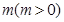
元奖金．假设顾客每次抽奖时获奖与否的概率都是
，
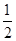（Ⅰ）求选出的4种不同型号商品中，洗衣机、电视机、空调都至少有一种型号的概率；
（Ⅱ）（文科）若顾客购买两种不同型号的商品，求中奖奖金至少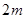
元的概率；
（理科）设顾客在三次抽奖中所获得的奖金总额（单位：元）为随机变量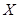
.请写出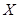的分布列，并求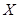的数学期望；
（Ⅲ）（理科）在（Ⅱ）的条件下，问该店若想采用此促销方案获利，则每次中奖奖金要低于多少元？
方程
在
上有解，命题
只有一个实数
满足不等式
，若命题“
”是假命题，求实数
的取值范围．
的最小正周期为
．
的值及函数
的单调递增区间；
时，求函数
．
的定义域；
，求
的值；
是第四象限角，求
的值．
．
时，求
在区间
上的最值；
时，有
恒成立，求
的取值范围．
为自然对数的底数
．
的最小值；
对任意的
恒成立，求实数
的值．