如图,在直三棱柱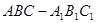 中,
中,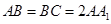 ,
, ,
, 是
是 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面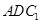 ; (Ⅱ)求二面角
; (Ⅱ)求二面角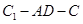 的余弦值;
的余弦值;
(Ⅲ)(理科)试问线段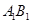 上是否存在点
上是否存在点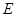 ,使
,使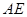 与
与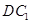 成
成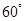 角?若存在,确定
角?若存在,确定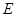 点位置,若不存在,说明理由.
点位置,若不存在,说明理由. 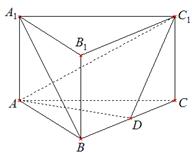
(12分)直角梯形ABCD中, ∠DAB=90°,AD//BC,
AB="2," AD=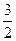 , BC=
, BC= ,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足:
,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足: ,问是否存在不平行AB,的直线
,问是否存在不平行AB,的直线 与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线
与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线 的斜率
的斜率 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
(12分)已知AB是椭圆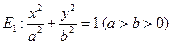 的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点
的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点 . (1)设双曲线E2的离心率为
. (1)设双曲线E2的离心率为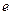 ,求
,求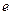 关于
关于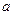 的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
(13分)如图(3):四面体D—ABC中,DB⊥面ABC, ∠DAB="30°,∠BAC=45°," ∠ACB=90°.BC=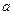 .
.
(1)点A与面BCD的距离; (2)AB与CD成的角的余弦值.
(13分)已知点A(2,8),B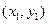 ,C
,C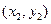 都在抛物线
都在抛物线 上,△ABC的重心与此抛物线E的焦点F重合. (1)写出抛物线E的方程及焦点坐标; (2)求线段BC的中点M的坐标及BC边所在的直线方程.
上,△ABC的重心与此抛物线E的焦点F重合. (1)写出抛物线E的方程及焦点坐标; (2)求线段BC的中点M的坐标及BC边所在的直线方程.
(13分)如图(2):PA⊥面ABCD,CD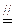 2AB,
2AB,
∠DAB=90°,E为PC的中点.
(1)证明:BE//面PAD;
(2)若PA=AD,证明:BE⊥面PDC.