某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革的关系，随机抽取了100名员工进行调查，其中支持企业改革的调查者中，工作积极的46人，工作一般的35人，而不太赞成企业改革的调查者中，工作积极的4人，工作一般的15人.
(1) 根据以上数据建立一个
的列联表；
(2) 对于人力资源部的研究项目，根据以上数据可以认为企业的全体员工对待企业改革的态度与其工作积极性是否有关系？
参考公式:
（其中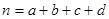
）
 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知函数
．
（1）若
，求函数
的极小值；
（2）设函数
，试问：在定义域内是否存在三个不同的自变量
使得
的值相等，若存在，请求出
的范围，若不存在，请说明理由？
已知函数f(x)＝x3－3x2＋2x
（1）在
处的切线平行于直线
，求点的坐标；
（2）求过原点的切线方程．
在平面直角坐标系
中，已知动点
到点
的距离为
，到
轴的距离为
，且
．
（1）求点
的轨迹
的方程；
（2） 若直线
斜率为1且过点
，其与轨迹交于点
，求
的值．
设函数f(x)＝2x3－3(a－1)x2＋1，其中a≥1．求函数f(x)的单调区间和极值．
如图，边长为1的正三角形
所在平面与直角梯形
所在平面垂直，且
，
，
，
，
、
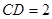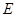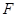分别是线段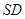
、
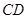的中点．
（1）求证：平面
平面
；
（2）求二面角
的余弦值．