如图,边长为1的正三角形 所在平面与直角梯形
所在平面与直角梯形 所在平面垂直,且
所在平面垂直,且 ,
, ,
, ,
,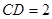 ,
, 、
、 分别是线段
分别是线段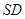 、
、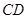 的中点.
的中点.
(1)求证:平面 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
已知椭圆
 的离心率为
的离心率为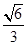 ,一个焦点为
,一个焦点为 .
.
(Ⅰ)求椭圆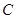 的方程;
的方程;
(Ⅱ)设直线 交椭圆
交椭圆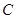 于
于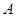 ,
, 两点,若点
两点,若点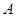 ,
, 都在以点
都在以点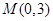 为圆心的圆上,求
为圆心的圆上,求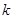 的值.
的值.
某少数民族的刺绣有着悠久的历史,如右图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含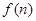 个小正方形.
个小正方形.
(1)求出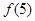 的值;
的值;
(2)利用合情推理的“归纳推理思想”,归纳出 与
与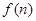 之间的关系式,并根据你得到的关系式求出
之间的关系式,并根据你得到的关系式求出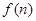 的表达式;
的表达式;
(3)求 的值。
的值。
已知双曲线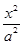 -
- =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e=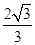 ,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是
,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是 .
.
(1)求双曲线的方程;
(2)过点B作直线m交双曲线于M、N两点,若 ·
· =-23,求直线m的方程.
=-23,求直线m的方程.
已知函数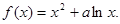
(1)当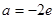 时,求函数
时,求函数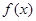 的单调区间和极值;
的单调区间和极值;
(2)若函数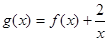 在[1,4]上是减函数,求实数
在[1,4]上是减函数,求实数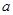 的取值范围
的取值范围
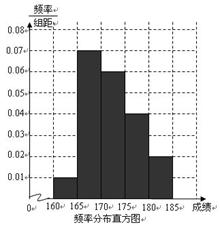
某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组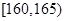 ,第2组
,第2组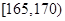 ,第3组
,第3组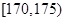 ,第4组
,第4组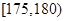 ,第5组
,第5组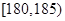 ,得到的频率分布直方图如图所示。
,得到的频率分布直方图如图所示。
(1)求第3、4、5组的频率;
(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率。