如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线;
(3)若过A,D,C三点的圆的半径为3,则线段BC上是否存在一点P,使得以P,D, B为顶点的三角形与△BCO相似?若存在,求出DP的长;若不存在,请说明理由.
某挖掘机的底座高 米,动臂 米, 米, 与 的固定夹角 .初始位置如图1,斗杆顶点 与铲斗顶点 所在直线 垂直地面 于点 ,测得 (示意图 .工作时如图3,动臂 会绕点 转动,当点 , , 在同一直线时,斗杆顶点 升至最高点(示意图 .
(1)求挖掘机在初始位置时动臂 与 的夹角 的度数.
(2)问斗杆顶点 的最高点比初始位置高了多少米?(精确到0.1米)
(参考数据: , , , ,

在“创全国文明城市”活动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中 、 两小区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
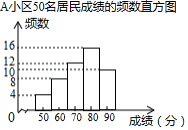
[信息一] 小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
[信息二]图中,从左往右第四组的成绩如下
|
75 |
75 |
79 |
79 |
79 |
79 |
80 |
80 |
|
81 |
82 |
82 |
83 |
83 |
84 |
84 |
84 |
[信息三] 、 两小区各50名居民成绩的平均数、中位数、众数、优秀率 分及以上为优秀)、方差等数据如下(部分空缺)
|
小区 |
平均数 |
中位数 |
众数 |
优秀率 |
方差 |
|
|
75.1 |
79 |
|
277 |
|
|
|
75.1 |
77 |
76 |
|
211 |
根据以上信息,回答下列问题:
(1)求 小区50名居民成绩的中位数.
(2)请估计 小区500名居民中能超过平均数的有多少人?
(3)请尽量从多个角度比较、分析 , 两小区居民掌握垃圾分类知识的情况.
在 的方格纸中,点 , , 都在格点上,按要求画图:
(1)在图1中找一个格点 ,使以点 , , , 为顶点的四边形是平行四边形.
(2)在图2中仅用无刻度的直尺,把线段 三等分(保留画图痕迹,不写画法).

如图,在直角坐标系中,已知点 ,等边三角形 的顶点 在反比例函数 的图象上.
(1)求反比例函数的表达式.
(2)把 向右平移 个单位长度,对应得到△ 当这个函数图象经过△ 一边的中点时,求 的值.

如图,在矩形 中,点 , 在对角线 .请添加一个条件,使得结论“ ”成立,并加以证明.
