（本小题满分12分）如图，在平面直角坐标系中，直线
：
与
轴交于点
，与
轴交于点
，抛物线
过点、点，且与轴的另一交点为
，其中
＞0，又点
是抛物线的对称轴
上一动点．
（1）求点的坐标，并在图1中的
上找一点
，使到点与点的距离之和最小；
（2）若△
周长的最小值为
，求抛物线的解析式及顶点
的坐标；
（3）如图2，在线段
上有一动点
以每秒2个单位的速度从点向点
移动(不与端点、重合)，过点作
∥
交轴于点
,设移动的时间为
秒，试把△
的面积
表示成时间的函数，当为何值时，有最大值，并求出最大值.
化简题（每小题4分，共8分）
2（x－3y）－（2y-x）
如图，△DEF是△ABC经过某种变换得到的图形，点A与点D，点B与点E，点C与点F分别是对应点，观察点与点的坐标之间的关系，解答下列问题：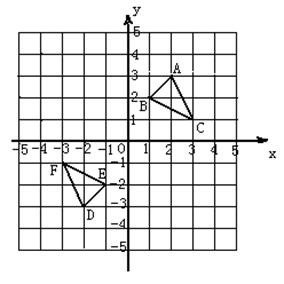
（1）分别写出点A与点D，点B与点E，点C与点F的坐标，并说说对应点的坐标有哪些特征；
（2）若点P（a＋3，4－b）与点Q（2a，2b－3）也是通过上述变换得到的对应点，求a、b的值。
如图所示,在△ABC中,AD⊥BC于D,AE平分∠BAC(∠C>∠B),试说明∠EAD=
(∠C-∠B).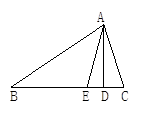
已知，如图在平面直角坐标系中，S△ABC=24，OA=OB，BC=12，求△ABC三个顶点的坐标.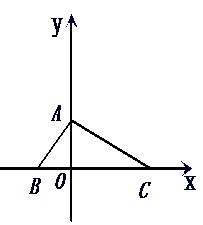 
作图题：在下图中平移三角形ABC，使点A移到点D，点B和点C应移到什么位置？请在图中画出平移后图形（保留作图痕迹）。