已知函数 =
= ,
, =alnx,a
=alnx,a R。
R。
(1) 若曲线y= 与曲线y=
与曲线y= 相交,且在交点处有相同的切线,求a的值及该切线的方程;
相交,且在交点处有相同的切线,求a的值及该切线的方程;
(2)设函数h(x)=  ,当h(x)存在最小之时,求其最小值
,当h(x)存在最小之时,求其最小值 的解析式;
的解析式;
(3)对(2)中的 ,证明:当a
,证明:当a (0,+
(0,+ )时,
)时,
 1.
1.
(本小题12分)
一个商场经销某种商品,根据以往资料统计,每位顾客采用的分期付款次数 的分布列为:
的分布列为:
 |
1 |
2 |
3 |
4 |
5 |
 |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;采用2期或3期付款,其利润为250元;采用4期或5期付款,其利润为300元. 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(Ⅰ)求购买该商品的3位顾客中,至少有1位采用1期付款的概率;
(Ⅱ)求 的分布列及期望
的分布列及期望 .
.
(本小题12分)
已知A, B,C为锐角
B,C为锐角 的三个内角,向量
的三个内角,向量
 ,
,
 ,且
,且 .
.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)求 取最大值时角
取最大值时角 的大小.
的大小.
(本小题满分12分)
如图, 在三棱柱 中,
中,  底面
底面 ,
, ,
,  ,
, , 点D是
, 点D是 的中点.
的中点.
(Ⅰ) 求证 ; (Ⅱ) 求证
; (Ⅱ) 求证 ∥平面
∥平面 .
.
(本小题满分12分)
已知函数 (
( ∈R).
∈R).
(Ⅰ)试给出 的一个值,并画出此时函数的图象;
的一个值,并画出此时函数的图象;
(Ⅱ)若函数 f (x) 在 上具有单调性,求
上具有单调性,求 的取值范围
的取值范围
(本小题满分10分)
设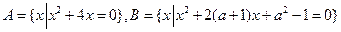 ,其中
,其中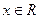 ,如果
,如果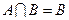 ,求实数
,求实数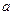 的取值范围
的取值范围