某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取
高二年级20名学生某次考试成绩,列出如下所示2×2列联表:
| 数学成绩 物理成绩 |
优秀 |
不优秀 |
合计 |
| 优秀 |
5 |
2 |
7 |
| 不优秀 |
1 |
12 |
13 |
| 合计 |
6 |
14 |
20 |
(1)根据题中表格的数据计算,你有多少的把握认为学生的数学成绩与物理成绩之间有关系?
(2)若按下面的方法从这20人(序号1,2,3,…,20)中抽取1人来了解有关情况:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:①抽到12号的概率;②抽到“无效序号(序号大于20)”的概率.
参考公式: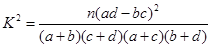 ,其中
,其中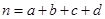 )
)
临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
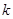 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
节日期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段




 后得到如下图所示的频率分布直方图.
后得到如下图所示的频率分布直方图.
(Ⅰ)此调查公司在采样中用到的是什么抽样方法?
(Ⅱ)求这40辆小型车辆车速的众数和中位数的估计值.
(Ⅲ)若从车速在 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在 的车辆数
的车辆数 的分布列及
的分布列及
数学期望.
如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形, ,
, 为
为 的中点,
的中点, .
.
(Ⅰ)点 在线段
在线段 上,
上, ,试确定
,试确定 的值,使得
的值,使得 平面
平面 ;
;
(Ⅱ)在(Ⅰ)的条件下,若平面
 面
面 ,求二面角
,求二面角 的大小.
的大小.
已知数列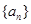 是等差数列,
是等差数列,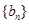 是等比数列,且
是等比数列,且 ,
, ,
, .
.
(Ⅰ)求数列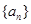 和
和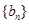 的通项公式
的通项公式
(Ⅱ)数列 满足
满足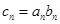 ,求数列
,求数列 的前
的前 项和
项和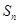 .
.
设角 是
是 的三个内角,已知向量
的三个内角,已知向量 ,
, ,且
,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若向量 ,试求
,试求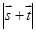 的取值范围
的取值范围
(本小题满分10分)(选修4-5不等式选讲)
设函数 .
.
求证:(1)当 时,不等式
时,不等式 成立.
成立.
(2)关于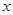 的不等式
的不等式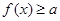 在R上恒成立,求实数
在R上恒成立,求实数 的最大值.
的最大值.