在
中,角
所对的边分别为
,且满足
.
(1)求角
的大小;
(2)求
的最大值,并求取得最大值时角
的大小.
已知函数 (a是常数,a∈R)
(a是常数,a∈R)
(1)当a=1时求不等式 的解集.
的解集.
(2)如果函数 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围.
已知曲线 (
( 为参数),曲线
为参数),曲线 ,将
,将 的横坐标伸长为原来的2倍,纵坐标缩短为原来的
的横坐标伸长为原来的2倍,纵坐标缩短为原来的 得到曲线
得到曲线 .
.
(1)求曲线 的普通方程,曲线
的普通方程,曲线 的直角坐标方程;
的直角坐标方程;
(2)若点P为曲线 上的任意一点,Q为曲线
上的任意一点,Q为曲线 上的任意一点,求线段
上的任意一点,求线段 的最小值,并求此时的P的坐标.
的最小值,并求此时的P的坐标.
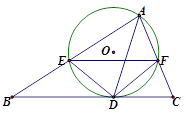
如图,在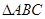 中,
中,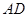 是的∠A的平分线,圆
是的∠A的平分线,圆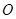 经过点
经过点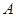 与
与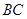 切于点
切于点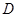 ,与
,与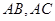 相交于
相交于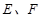 ,连结
,连结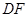 ,
,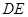 .
.
(1)求证: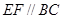 ;(2)求证:
;(2)求证: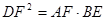 .
.
设椭圆C1: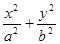 =1(a>b>0)的左、右焦点分别为为
=1(a>b>0)的左、右焦点分别为为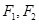 ,
,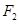 恰是抛物线C2:
恰是抛物线C2: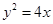 的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
的焦点,点M为C1与C2在第一象限的交点,且|MF2|=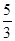 .
.
(1)求C1的方程;
(2)平面上的点N满足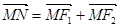 ,直线l∥MN,且与C1交于A,B两点,若
,直线l∥MN,且与C1交于A,B两点,若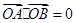 ,求直线l的方程.
,求直线l的方程.