已知函数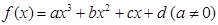 的图象经过原点,
的图象经过原点,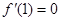 若
若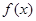 在
在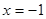 取得极大值2。
取得极大值2。
(1)求函数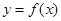 的解析式;
的解析式;
(2)若对任意的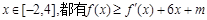 ,求
,求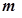 的最大值。
的最大值。
第26届世界大学生夏季运动会将于2011年8月12日至23日在深圳举行,为了搞好接待工作,组委会在某学院招募了 名男志愿者和
名男志愿者和 名女志愿者,调查发现,这
名女志愿者,调查发现,这 名志愿者的身高如下:(单位:cm)
名志愿者的身高如下:(单位:cm)
若身高在 cm以上(包括
cm以上(包括 cm)定义为“高个子”,身高在
cm)定义为“高个子”,身高在 cm以下定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
cm以下定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取 人,再从这
人,再从这 人中选
人中选 人,则至少有一人是“高个子”的概率是多少?
人,则至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选 名志愿者,用
名志愿者,用 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.
已知向量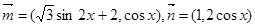 ,设函数
,设函数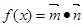 。
。
(1)求 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在 中,
中,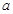 、
、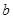 、
、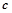 分别是角
分别是角 、
、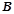 、
、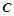 的对边,若
的对边,若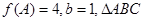 的面积为
的面积为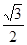 ,求
,求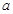 的值。
的值。
在△ABC中,内角A,B,C所对的边分别为a,b,c.向量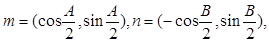 且满足
且满足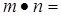
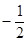 .
.
(1)求角C的大小;
(2)若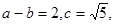 求△ABC的面积.
求△ABC的面积.
已知数列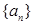 的前n项和为
的前n项和为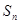 ,且
,且 .
.
(1) 求数列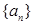 的通项公式;
的通项公式;
(2) 令
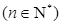 ,求数列
,求数列 的前
的前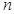 项和
项和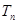 .
.
△ABC中,内角A,B,C所对的边分别为a,b,c.若 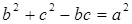 且
且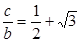 .
.
(1)求角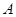 的值;
的值;
(2)求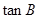 的值.
的值.