如图所示,一端封闭的两条平行光滑长导轨相距L,距左端L处的右侧一段弯成半径为 的四分之一圆弧,圆弧导轨的左、右两段处于高度相差
的四分之一圆弧,圆弧导轨的左、右两段处于高度相差 的水平面上。以弧形导轨的末端点O为坐标原点,水平向右为x轴正方向,建立Ox坐标轴。圆弧导轨所在区域无磁场;左段区域存在空间上均匀分布,但随时间t均匀变化的磁场B(t),如图2所示;右段区域存在磁感应强度大小不随时间变化,只沿x方向均匀变化的磁场B(x),如图3所示;磁场B(t)和B(x)的方向均竖直向上。在圆弧导轨最上端,放置一质量为m的金属棒ab,与导轨左段形成闭合回路,金属棒由静止开始下滑时左段磁场B(t)开始变化,金属棒与导轨始终接触良好,经过时间t0金属棒恰好滑到圆弧导轨底端。已知金属棒在回路中的电阻为R,导轨电阻不计,重力加速度为g。
的水平面上。以弧形导轨的末端点O为坐标原点,水平向右为x轴正方向,建立Ox坐标轴。圆弧导轨所在区域无磁场;左段区域存在空间上均匀分布,但随时间t均匀变化的磁场B(t),如图2所示;右段区域存在磁感应强度大小不随时间变化,只沿x方向均匀变化的磁场B(x),如图3所示;磁场B(t)和B(x)的方向均竖直向上。在圆弧导轨最上端,放置一质量为m的金属棒ab,与导轨左段形成闭合回路,金属棒由静止开始下滑时左段磁场B(t)开始变化,金属棒与导轨始终接触良好,经过时间t0金属棒恰好滑到圆弧导轨底端。已知金属棒在回路中的电阻为R,导轨电阻不计,重力加速度为g。
(1)求金属棒在圆弧轨道上滑动过程中,回路中产生的感应电动势E;
(2)如果根据已知条件,金属棒能离开右段磁场B(x)区域,离开时的速度为v,求金属棒从开始滑动到离开右段磁场过程中产生的焦耳热Q;
(3)如果根据已知条件,金属棒滑行到x=x1,位置时停下来,
a.求金属棒在水平轨道上滑动过程中遁过导体棒的电荷量q;
b.通过计算,确定金属棒在全部运动过程中感应电流最大时的位置。
如图,竖直平面内有一直角形内径相同的 细玻璃管,A端封闭,C端开口,AB="BC" =l0,且此时A、C端等高。管内水银总长度为l0,玻璃管AB内封闭长为l0/2的空气柱。已知大气压强为l0汞柱髙。如果使玻璃管绕B点在竖直平面内顺时针缓慢地转动至BC管水平,求此时AB管内气体 的压强为多少汞柱高?管内封入的气体可视为理想气体且温度不变。
如图甲所示,在PQ左侧空间有方向斜向右上的匀强电场E1在PQ右侧空间 有一竖直向上的匀强电场E2="0.4N/C,还有垂直纸面向里的匀强磁场B(图甲中未画" 出)和水平向右的匀强电场E3 (图甲中未画出),B和E3随时间变化的情况如图乙所 示,MN为距PQ边界2.295m的竖直墙壁,现有一带正电的微粒质量为4x1O 7kg电量为1xlO 5C,从左侧电场中距PQ边界 m的A处无初速释放后,沿直线以1m/s速度垂直PQ边界进入右侧场区,设进入右侧场时刻t=0,取g = lOm/s2.求:
m的A处无初速释放后,沿直线以1m/s速度垂直PQ边界进入右侧场区,设进入右侧场时刻t=0,取g = lOm/s2.求:
(1)PQ左侧匀强电场的电场强度E1,的大小及方向。(sin37°=0.6);
(2)带电微粒在PQ右侧场区中运动了1.5s时的速度的大小及方向;
(3)带电微粒在PQ右侧场区中运动多长时间与墙壁碰撞?( )
)
在某一个探究实验中,实验员将某物体以某一确定的初速率v。沿斜面向上推 出(斜面足够长且与水平方向的倾角θ可调节),设物体在斜面上能达到的最大位移为 sm实验测得sm与斜面倾角θ的关系如右图所示,g取10m/s2,求:物体的初速率v0 和物体与斜面间的动摩擦因数

(15分)如图甲所示为一倾角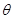 =30°的足够长的绝缘斜面,在斜面上P点的上方是光滑的,P点下方粗糙,整个斜面体处在一个交变的电磁场中,电、磁场的变化规律如图乙和丙所示,磁场方向以垂直纸面向外为正,而电场的方向以竖直向下为正,其中
=30°的足够长的绝缘斜面,在斜面上P点的上方是光滑的,P点下方粗糙,整个斜面体处在一个交变的电磁场中,电、磁场的变化规律如图乙和丙所示,磁场方向以垂直纸面向外为正,而电场的方向以竖直向下为正,其中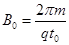 ,
,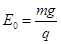 ,现有一个可视为质点、带负电的小物块(其质量为
,现有一个可视为质点、带负电的小物块(其质量为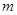 、带电量大小为
、带电量大小为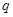 ),从t=0时刻由静止开始从A点沿斜面下滑,在t=3t0时刻刚好到达斜面上的P点,在以后运动过程中的某时刻开始,物块运动的速率保持不变.若已知斜面粗糙部分与物块间的动摩擦因素为
),从t=0时刻由静止开始从A点沿斜面下滑,在t=3t0时刻刚好到达斜面上的P点,在以后运动过程中的某时刻开始,物块运动的速率保持不变.若已知斜面粗糙部分与物块间的动摩擦因素为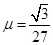 ,求:
,求: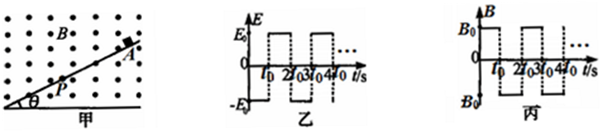
(1)小球在t0时刻的速度及AP的长度;
(2)在整个运动过程中物块离开斜面的最大距离为多少?
(12分)如图所示,在倾角为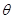 的足够长的斜面上,有一质量为M的长木板.开始时长木板上有一质量为m的小铁块(视为质点)以相对地面的初速度
的足够长的斜面上,有一质量为M的长木板.开始时长木板上有一质量为m的小铁块(视为质点)以相对地面的初速度 从长木板的中点沿长木板向下滑动,同时长木板在沿斜面向上的拉力作用下始终作速度为
从长木板的中点沿长木板向下滑动,同时长木板在沿斜面向上的拉力作用下始终作速度为 的匀速运动(已知
的匀速运动(已知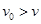 ),小铁块最终跟长木板一起向上做匀速运动.已知小铁块与木板、木板与斜面间的动摩擦因数均为μ(μ>tan
),小铁块最终跟长木板一起向上做匀速运动.已知小铁块与木板、木板与斜面间的动摩擦因数均为μ(μ>tan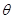 ),试求:
),试求:
(1)小铁块在长木板上滑动时的加速度?
(2)长木板至少多长?