右图为函数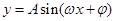
的一段图象.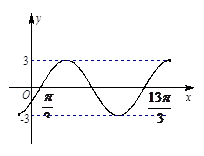
(1)请写出这个函数的一个解析式；
(2)求与（1）中函数图象关于直线
对称的函数图象的解析式，并作出它一个周期内的简图．
若a、b、c均为实数，且
，求证：a、b、c中至少有一个大于0．
关于x的不等式
与指数函数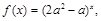
若命题“p的解集为
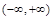或
在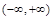内是增函数”是真命题，求实数
的取值范围．
写出下列各组命题的“或”命题，并判断其真假
①p：2=2；q：2＞2．
②p：正方形的对角线互相垂直；q：矩形的对角线互相平分．
分别指出由下列各组命题构成的逻辑关联词“或”、“且”的真假．
（1）p: 梯形有一组对边平行；q：梯形有一组对边相等．
（2）p: 1是方程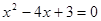
的解；q：3是方程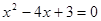的解．
（3）p: 不等式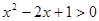
解集为R；q: 不等式
解集为Æ．
（4）p: 
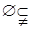
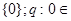Æ
已知
是等差数列，d为公差且不为0，a1和d均为实数，它的前n项和记作Sn，设集合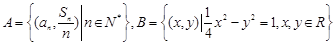
．试问下列命题是否是真命题，如果是真命题，请给予证明；如果是假命题，请举反例说明．
（1）若以集合A中的元素作为点的坐标，则这些点都在同一条直线上；
（2）
至多有一个元素；
（3）当a1≠0时，一定有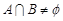
．