已知数列{an}的各项均为正数,其前n项和为Sn,且 -1,
-1, ,数列
,数列 ,
, ,
, ……,
……,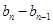 是首项为1,公比为
是首项为1,公比为 的等比数列。
的等比数列。
(I)求证:数列{an}是等差数列;
(II)若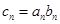 ,求数列{cn}的前n项和Tn。
,求数列{cn}的前n项和Tn。
(本题满分14分) 在△ABC中,角A,B,C所对的边分别为a,b,c,已知
tan (A+B)=2.
(Ⅰ) 求sin C的值;
(Ⅱ) 当a=1,c= 时,求b的值.
时,求b的值.
已知函数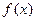 =
=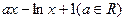 ,
, .
.
(1)求函数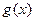 在区间
在区间 上的值域T;
上的值域T;
(2)是否存在实数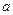 ,对任意给定的集合T中的元素t,在区间
,对任意给定的集合T中的元素t,在区间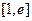 上总存在两个不同的
上总存在两个不同的 ,使得
,使得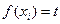 成立.若存在,求出
成立.若存在,求出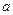 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(3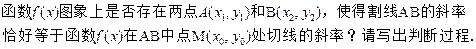
设数列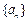 是有穷等差数列,给出下面数表:
是有穷等差数列,给出下面数表:
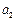
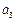 ……
……
 第1行
第1行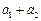
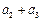 ……
…… 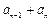 第2行
第2行
… … …
……
… 第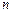 行
行
上表共有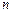 行,其中第1行的
行,其中第1行的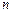 个数为
个数为 ,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为
,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为 .
.
(1)求证:数列 成等比数列;
成等比数列;
(2)若 ,求和
,求和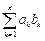 .
.
某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),年
产量不足80千件时,C(x)= 2+10x(万元);当年产量不小于80千件时,
2+10x(万元);当年产量不小于80千件时,
C(x)=51x+ -1450(万元).通过市场分析,若每件售价为500元时,该厂当年生产
-1450(万元).通过市场分析,若每件售价为500元时,该厂当年生产
的该产品能全部销售完.
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一产品的生产中所获利润最大,最大利润是多少?
已知函数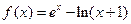 .(e是自然对数的底数)
.(e是自然对数的底数)
(1)判断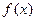 在
在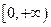 上是否是单调函数,并写出
上是否是单调函数,并写出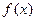 在该区间上的最小值;
在该区间上的最小值;
(2)证明: