已知椭圆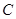 :
: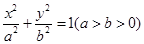 的离心率为
的离心率为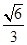 ,过椭圆
,过椭圆 的右焦点F且斜率为1的直线
的右焦点F且斜率为1的直线 交椭圆于
交椭圆于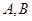 两点,
两点,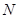 为弦
为弦 的中点,
的中点,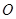 为坐标原点。
为坐标原点。
(1)求直线 的斜率
的斜率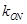 ;
;
(2)对于椭圆上的任意一点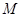 ,试证:总存在
,试证:总存在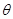 ,使得等式
,使得等式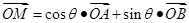 成立.
成立.
(本小题共14分)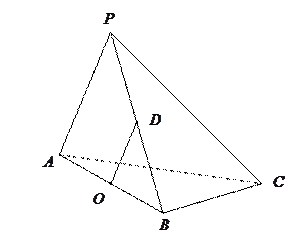
在三棱锥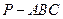 中,
中,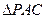 和
和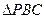 是边长为
是边长为 的等边三角形,
的等边三角形,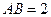 ,
,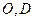 分别是
分别是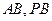 的中点.
的中点.
(Ⅰ)求证: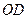 ∥平面
∥平面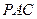 ;
;
(Ⅱ)求证:平面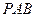 ⊥平面
⊥平面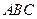 ;
;
(Ⅲ)求三棱锥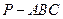 的体积.
的体积.
(本小题共12分)
已知函数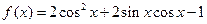 .
.
(Ⅰ)求函数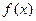 的最小正周期;
的最小正周期;
(Ⅱ)求函数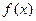 在
在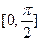 上的最大值与最小值.
上的最大值与最小值.
设函数f(x)=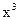 -6x+5,X
-6x+5,X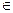 R
R
(1) 求函数f(x)的单调区间和极值
(2) 若关于x的方程f(x)=a有三个不同实根,求实数a的范围.
(3) 已知当x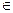 (1,+∞)时,f(x)≥K(x-1)恒成立,求实数K的取值范围。
(1,+∞)时,f(x)≥K(x-1)恒成立,求实数K的取值范围。
已知向量a=(sinX, ),b=(cosX,﹣1)
),b=(cosX,﹣1)
(1) 当a∥b时,求2cos2X-sin2X的值
(2)求f(x)=(a+b)·b的值域
F1,F2是双曲线的左右焦点,P是双曲线上一点,且∠F1PF2=600,S△PF1 F2=12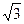
又离心率为2,求双曲线方程。