六名学生需依次进行身体体能和外语两个项目的训练及考核。每个项目只有一次补考机会,补考不合格者不能进入下一个项目的训练(即淘汰),若每个学生身体体能考核合格的概率是 ,外语考核合格的概率是
,外语考核合格的概率是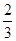 ,假设每一次考试是否合格互不影响。
,假设每一次考试是否合格互不影响。
①求某个学生不被淘汰的概率。
②求6名学生至多有两名被淘汰的概率
③假设某学生不放弃每一次考核的机会,用 表示其参加补考的次数,求随机变量
表示其参加补考的次数,求随机变量 的分布列和数学期望。
的分布列和数学期望。
已知数列 中,
中, ,对
,对 总有
总有 成立,
成立,
(1)计算 的值;
的值;
(2)根据(1)的结果猜想数列的通项 ,并用数学归纳法证明
,并用数学归纳法证明
已知复数 ,(
,( ,
, 为虚单位)。
为虚单位)。
(1)若 为实数,求
为实数,求 的值;
的值;
(2)若复数 对应的点在第四象限,求实数
对应的点在第四象限,求实数 的取值范围
的取值范围
某工厂有A、B两种配件生产甲、乙两种产品,每生产一种甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天8h计算,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
已知函数 在点
在点 处取得极小值-4,使其导数
处取得极小值-4,使其导数 的
的 的取值范围为
的取值范围为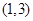 ,求:
,求:
(1) 的解析式;
的解析式;
(2) ,求
,求 的最大值;
的最大值;
已知: ,
, ,
, 是的内角,
是的内角, ,
,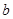 ,
, 分别是其对边长,向量,,.
分别是其对边长,向量,,.
(1)求角A的大小;
(2)若求的长.