在平面直角坐标系中,已知某点 ,直线
,直线 .求证:点P到直线
.求证:点P到直线 的距离
的距离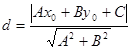
求sin220°+cos250°+sin20°cos50°的值.
已知函数y= sinx+cosx,x∈R.
sinx+cosx,x∈R.
(1)当函数y取得最大值时,求自变量x的集合;
(2)该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
已知函数y=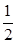 cos2x+
cos2x+ sinxcosx+1,x∈R.
sinxcosx+1,x∈R.
(1)当函数y取得最大值时,求自变量x的集合;
(2)该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
作出函数y=|sinx|+|cosx|,x∈[0,π]的图象,并写出函数的值域.
如图,某地一天从6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)求这段时间的最大温差;
(2)写出这段曲线的函数解析式.