如图,某地一天从6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)求这段时间的最大温差;
(2)写出这段曲线的函数解析式.
(本题10分)已知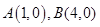 ,动点
,动点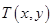 满足
满足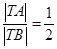 ,设动点
,设动点 的轨迹是曲线
的轨迹是曲线 ,直线
,直线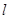 :
: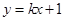 与曲线
与曲线 交于
交于 两点.(1)求曲线
两点.(1)求曲线 的方程;
的方程;
(2)若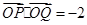 ,求实数
,求实数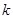 的值;
的值;
(3)过点 作直线
作直线 与
与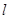 垂直,且直线
垂直,且直线 与曲线
与曲线 交于
交于 两点,求四边形
两点,求四边形 面积的最大值.
面积的最大值.
如图,已知四棱锥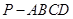 底面
底面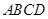 为菱形,
为菱形,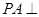 平面
平面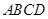 ,
,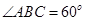 ,
, 分别是
分别是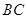 、
、 的中点.
的中点.
(1)证明:
(2)设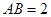 , 若
, 若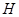 为线段
为线段 上的动点,
上的动点,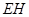 与平面
与平面 所成的最大角的正切值为
所成的最大角的正切值为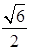 ,求此时异面直线AE和CH所成的角.
,求此时异面直线AE和CH所成的角.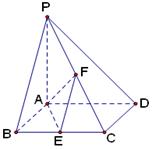
(本题满分10分) 如图,在平行四边形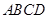 中,
中,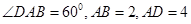 ,将
,将 沿
沿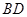 折起到
折起到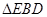 的位置,使平面
的位置,使平面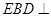 平面
平面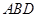 .
.
(1)求二面角E-AB-D的大小;
(2)求四面体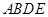 的表面积和体积.
的表面积和体积.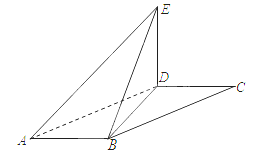
在长方体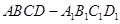 中,
中,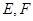 分别是
分别是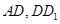 的中点,
的中点,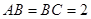 ,
,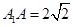 .
.
(Ⅰ)求证: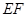 //平面
//平面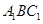 ;
;
(Ⅱ)在线段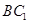 上是否存在点
上是否存在点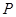 ,使直线
,使直线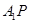 与
与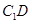 垂直,
垂直,
如果存在,求线段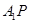 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.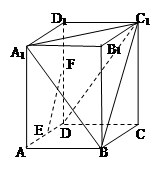
已知顶点在原点,焦点在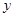 轴上的抛物线过点
轴上的抛物线过点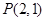 .
.
(1)求抛物线的标准方程;
(2)过点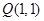 作直线交抛物线于
作直线交抛物线于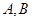 两点,使得
两点,使得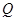 恰好平分线段
恰好平分线段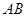 ,求直线
,求直线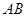 的方程
的方程