用平行于棱锥底面的平面去截棱锥,则截面与底面之间的部分叫棱台.如图,在四棱台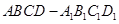 中,下底
中,下底 是边长为
是边长为 的正方形,上底
的正方形,上底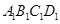 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱 ⊥平面
⊥平面 ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(II)求平面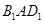 与平面
与平面 夹角的余弦值.
夹角的余弦值.
等差数列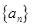 中,
中, ,公差
,公差 为整数,若
为整数,若 ,
, .
.
(1)求公差 的值; (2)求通项公式
的值; (2)求通项公式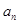 。
。
风景秀美的凤凰湖畔有四棵高大的银杏树,记做A、B、P、Q,欲测量P、Q两棵树和A、P两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得A、B两点间的距离为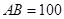 米,如图,同时也能测量出
米,如图,同时也能测量出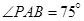 ,
, ,
, ,
, ,则P、Q两棵树和A、P两棵树之间的距离各为多少?
,则P、Q两棵树和A、P两棵树之间的距离各为多少?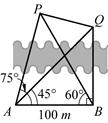
已知椭圆 :
: 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线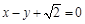 相切.
相切.
(1)求椭圆C的方程;
(2)设 ,
, 、
、 是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 于另一点
于另一点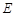 ,求直线
,求直线 的斜率的取值范围;
的斜率的取值范围;
(3)在(2)的条件下,证明直线 与
与 轴相交于定点.
轴相交于定点.
在直角坐标系中,射线OA: x-y=0(x≥0),
OB: x+2y=0(x≥0),过点P(1,0)作直线分别交射线OA、OB于A、B两点.
(1)当AB中点为P时,求直线AB的方程;
(2)当AB中点在直线 上时,求直线AB的方程.
上时,求直线AB的方程.
已知四棱锥P-ABCD的直观图(如图(1))及左视图(如图(2)),底面ABCD是边长为2的正方形,平面PAB⊥平面ABCD,PA=PB。
(1)求证:AD⊥PB;
(2)求异面直线PD与AB所成角的余弦值;
(3)求平面PAB与平面PCD所成锐二面角的大小.