某教研机构准备举行一次高中数学新课程研讨会,拟邀请50名使用不同版本的一线教师参加,使用不同版本教材的教师人数如下表所示
(I)从这50名教师中随机选出2名教师发言,求第一位发言的教师所使用版本是北大师大版的概率;
(II)设使用北师大版的5名教师中有3名男教师,2名女教师,若随机选出2名用北师大版的教师发言,求抽到男教师个数的分布列和期望.
(12分)古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有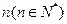 个圆盘依其半径大小,大的在下,小的在上套在
个圆盘依其半径大小,大的在下,小的在上套在 柱上,现要将套在
柱上,现要将套在 柱上的盘换到
柱上的盘换到 柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子
柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子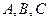 可供使用.
可供使用.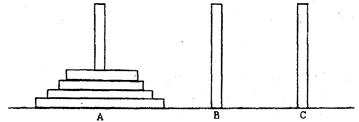
现用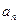 表示将
表示将 个圆盘全部从
个圆盘全部从
 柱上移到
柱上移到 柱上所至少需要移动的次数,回答下列问题:
柱上所至少需要移动的次数,回答下列问题:
(1)写出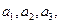 并求出
并求出 (2)记
(2)记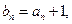 求和
求和
(其中 表示所有的积
表示所有的积 的和)
的和)
(3)证明:
(12分)如图,斜率为 1的直线过抛物线
1的直线过抛物线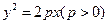 的焦点,与抛物线交于两点
的焦点,与抛物线交于两点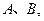 将
将 直线
直线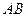 按向量
按向量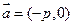 平移到
平移到
直线 为
为 上的动点.(1)若
上的动点.(1)若 求抛物线的方程;
求抛物线的方程;
(2)求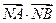 的最小值.
的最小值.
(12分)已知函数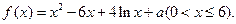 (1)求函数的单调区间;(2)
(1)求函数的单调区间;(2) 为何值时,方程
为何值时,方程 有三个不同的实根.
有三个不同的实根.
(13分)正项数列 的前
的前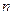 项和为
项和为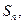 且
且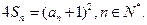
(1)试求数列 的通项公式;(2)设
的通项公式;(2)设 求数列
求数列 的前
的前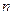 项和
项和
(13分)已知向量
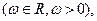 设函数
设函数 若
若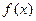 的最小正周期为
的最小正周期为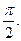 (1)求
(1)求 的值;(2)求
的值;(2)求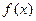 的单调区间.
的单调区间.