甲、乙两同学进行下棋比赛,约定每局胜者得1分,负者得0分(无平局),比赛进行到有一个人比对方多2分或比满8局时停止,设甲在每局中获胜的概率为 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为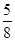 .
.
(I)如右图为统计这次比赛的局数n和甲、乙的总得分S,T的程序框图.其中如果甲获胜,输人a=l.b=0;如果乙获胜,则输人a=0,b=1.请问在①②两个判断框中应分别填写什么条件?
(Ⅱ)求p的值;
(Ⅲ)设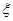 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量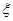 的分布列和
的分布列和

(本小题满分12分)
已知数列
 是等比数列
是等比数列 它的前
它的前  项和,若
项和,若 ,且
,且 与
与  的等差中项为
的等差中项为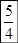 ,求
,求
(本小题满分10分)
已知函数 ,记
,记 的内角A,B,C的对边长分别为a,b,c,若
的内角A,B,C的对边长分别为a,b,c,若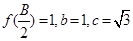 ,求a的值.
,求a的值.
、设函数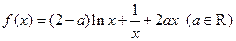 .
.
(Ⅰ)当 时,求
时,求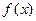 的极值;
的极值;
(Ⅱ)当 时,求
时,求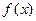 的单调区间;
的单调区间;
(Ⅲ)若对任意 及
及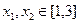 ,恒有
,恒有
成立,求 的取值范围.
的取值范围.
在平面直角坐标系 中,已知圆
中,已知圆 和圆
和圆 .
.
(1)若直线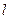 过点
过点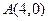 ,且被圆
,且被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线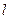 的方程;
的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线 和
和 ,它们分别与圆
,它们分别与圆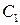 和圆
和圆 相交,且直线
相交,且直线 被圆
被圆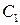 截得的弦长与直线
截得的弦长与直线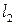 被圆
被圆 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
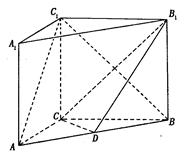
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
(I)求证:AC 1//平面CDB1;
(II)求二面角C1-AB-C的平面角的正切值。