已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C与直线l1:y=-x的一个交点的横坐标为8.
(1)求抛物线C的方程;
(2)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A、B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.
国家射击队的队员为在2010年亚运会上取得优异成绩,正在加紧备战,经过近期训练,某队员射击一次,命中7~10环的概率如下表所示:
| 命中环数 |
10环 |
9环 |
8环 |
7环 |
| 概率 |
0.32 |
0.28 |
0.18 |
0.12 |
求该射击队员射击一次
(1)射中9环或10环的概率;
(2)至少命中8环的概率;
(3)命中不足8环的概率.
已知两直线l1:mx+8y+n=0和l2:2x+my-1=0.试确定m、n的值,分别使
(1)l1与l2相交于点P(m,-1);
(2)l1∥l2;
(3)l1⊥l2且l1在y轴上的截距为-1.
甲、乙两名射击运动员,甲射击一次命中10环的概率为0.5,乙射击一次命中10环的概率为s,若他们独立的射击两次,设乙命中10环的次数为X,则EX=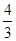 ,Y为甲与乙命中10环次数的差的绝对值.
,Y为甲与乙命中10环次数的差的绝对值.
求(1) s的值 (2) Y的分布列及期望.
已知函数f(x)=x2-(a+2)x+alnx(a∈R)。
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若a=4,y=f(x)的图像与直线y=m有三个交点,求m的取值范围。
已知数列{an}(n为正整数)是首项为a1,公比为q的等比数列.
(1)求和: ( i )a1C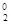 -a2C
-a2C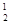 +a3C
+a3C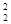 , ( ii )a1C
, ( ii )a1C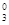 -a2C
-a2C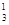 +a3C
+a3C -a4C
-a4C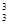 ;
;
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.