四棱锥P—ABCD中,底面ABCD是矩形,PA 底面ABCD,PA=" AB" =1,AD =2,点M是PB的中点,点N在BC边上移动.
底面ABCD,PA=" AB" =1,AD =2,点M是PB的中点,点N在BC边上移动.
(I)求证:当N是BC边的中点时,MN∥平面PAC;
(Ⅱ)证明,无论N点在BC边上何处,都有PN AM;
AM;
(Ⅲ)当BN等于何值时,PA与平面PDN所成角的大小为45 .
.
已知向量a=(1,2),b=(2,-2).
(1)设c=4a+b,求(b·c)a;
(2)若a+λb与a垂直,求λ的值;
(3)求向量a在b方向上的投影.
已知点G是△ABO的重心,M是AB边的中点.
(1)求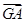 +
+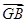 +
+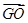 ;
;
(2)若PQ过△ABO的重心G,且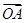 =a,
=a, =b,
=b,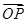 =ma,
=ma,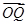 =nb,求证:
=nb,求证: +
+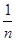 =3.
=3.
设i、j分别是平面直角坐标系Ox,Oy正方向上的单位向量,且 =-2i+mj,
=-2i+mj, =ni+j,
=ni+j,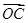 =5i-j,若点A、B、C在同一条直线上,且m=2n,求实数m、n的值.
=5i-j,若点A、B、C在同一条直线上,且m=2n,求实数m、n的值.
设a、b是不共线的两个非零向量,
(1)若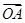 =2a-b,
=2a-b,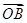 =3a+b,
=3a+b,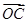 =a-3b,求证:A、B、C三点共线;
=a-3b,求证:A、B、C三点共线;
(2)若8a+kb与ka+2b共线,求实数k的值.
已知直线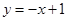 与椭圆
与椭圆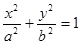
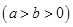 相交于A、B两点.
相交于A、B两点.
(1)若椭圆的离心率为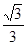 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;
(2)若向量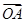 与向量
与向量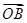 互相垂直(其中
互相垂直(其中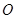 为坐标原点),当椭圆的离心率
为坐标原点),当椭圆的离心率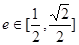 时,求椭圆长轴长的最大值.
时,求椭圆长轴长的最大值.