(本小题满分10分)选修4—4;坐标系与参数方程.
已知直线
 为参数), 曲线
为参数), 曲线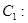
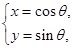 (
( 为参数).
为参数).
(Ⅰ)设 与
与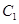 相交于
相交于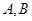 两点,求
两点,求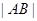 ;
;
(Ⅱ)若把曲线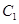 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的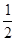 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的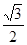 倍,得到曲线
倍,得到曲线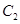 ,设点
,设点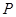 是曲线
是曲线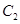 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
(本小题满分12分)
已知函数 .
.
(1)求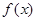 的单调递增区间;
的单调递增区间;
(2)在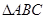 中,角
中,角 ,
,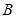 ,
,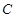 的对边分别为
的对边分别为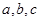 .已知
.已知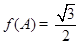 ,
, ,试判断
,试判断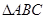 的形状.
的形状.
(本小题满分14分)已知函数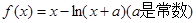 .
.
(1)求函数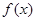 的单调区间;
的单调区间;
(2)当 处取得极值时,若关于
处取得极值时,若关于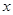 的方程
的方程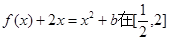 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)求证:当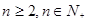 时,有
时,有
(本小题满分13分)
动圆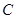 与定圆
与定圆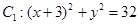 内切,与定圆
内切,与定圆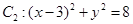 外切,A点坐标为
外切,A点坐标为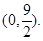
(1)求动圆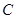 的圆心
的圆心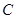 的轨迹方程和离心率;
的轨迹方程和离心率;
(2)若轨迹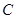 上的两点
上的两点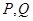 满足
满足 ,求
,求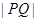 的值.
的值.
(本小题满分12分)如图,在三棱锥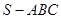 中,底面
中,底面 是边长为4的正三角形,平面
是边长为4的正三角形,平面
 ,M,N分别为AB,SB的中点.
,M,N分别为AB,SB的中点.
(1)求证: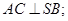
(2)求二面角 的余弦值.
的余弦值.
(本小题满分12分)
医生的专业能力参数K可有效衡量医生的综合能力,K越大,综合能力越强,并规定:能力参数K不少于30称为合格,不少于50称为优秀,某市卫生管理部门随机抽取300名医生进行专业能力参数考核,得到如图所示的能力参数K的频率颁布直方图: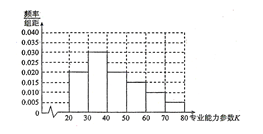
(1)求这个样本的合格率、优秀率,并估计能力参数K的平均值;
(2)现用分层抽样的方法从中抽出一个样本容量为20的样本,再从这20名医生中随机选出2名。
①求这2名医生的能力参数K为同一组的概率;
②设这2名医生中能力参数K为优秀的的人数为X,求随机变量X的分布列和期望。