(本小题满分12分)已知数列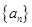 首项为1,
首项为1,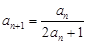 .
.
(1)证明:数列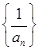 是等差数列,并求
是等差数列,并求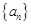 的通项公式;
的通项公式;
(2)记数列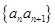 的前
的前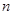 项和为
项和为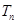 ,证明:
,证明: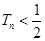 .
.
已知抛物线C:y2=4x.
(1)若椭圆左焦点及相应的准线与抛物线C的焦点F及准线l分别重合,试求椭圆短轴端点B与焦点F连线中点P的轨迹方程;
(2)若M(m,0)是x轴上的一定点,Q是(1)所求轨迹上任一点,试问|MQ|有无最小值?若有,求出其值;若没有,说明理由.
已知直线y=kx-1与双曲线x2-y2=1的左支交于A、B两点,若另一条直线l经过点P(-2,0)及线段AB的中点Q,求直线l在y轴上的截距b的取值范围.
如图,已知△P1OP2的面积为 ,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为
,P为线段P1P2的一个三等分点,求以直线OP1、OP2为渐近线且过点P的离心率为 的双曲线方程.
的双曲线方程. 
过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为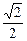 的椭圆C相交于A、B两点,直线y=
的椭圆C相交于A、B两点,直线y=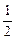 x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程. 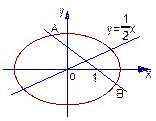
某电厂冷却塔的外形是如图所示的双曲线的一部分,绕其中轴(即双曲线的虚轴)旋转所成的曲面,其中A、A′是双曲线的顶点,C、C′是冷却塔上口直径的两个端点,B、B′是下底直径的两个端点,已知AA′="14" m,CC′="18" m,BB′="22" m,塔高20 m.建立坐标系并写出该双曲线方程.