已知抛物线C:y2=4x.
(1)若椭圆左焦点及相应的准线与抛物线C的焦点F及准线l分别重合，试求椭圆短轴端点B与焦点F连线中点P的轨迹方程；
(2)若M(m,0)是x轴上的一定点，Q是(1)所求轨迹上任一点，试问|MQ|有无最小值？若有，求出其值；若没有，说明理由.
(14分)已知数列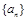
的首项
，
，
…．
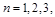(1)数列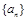的通项公式；
(2)求数列
的前
项和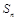
．
(14分)等差数列{an}中，公差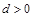
，其前
项和为
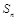，且满足
，
。
(1)求数列{an}的通项公式；
(2)构造一个新的数列{bn}，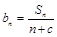
，若{bn}也是等差数列，求非零常数
．
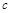(14分)一农民有基本农田2亩，根据往年经验，若种水稻，则每季每亩产量为400公斤，但需成本240元；若种花生，则每季每亩产量为100公斤，但成本只需80元。种花生每公斤可卖5元，稻米每公斤卖3元．现该农民手头有400元，两种作物各种多少，才能获得最大收益？
(14分)设条件p：(4x－3)2－1≤0；条件q：x2－(2m＋1)x＋m(m＋1)≤0，若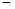
p是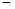q的必要不充分条件，求实数m的取值范围．
(12分)设集合A＝{x|－2－a<x<a，a>0}，命题p：1∈A，命题q：2∈A．若p∨q为真命题，p∧q为假命题，求a的取值范围．