(14分)已知数列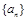 的首项
的首项 ,
, ,
,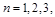 ….
….
(1)数列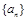 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和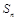 .
.
((本小题满分12分)
在数列 中,
中,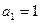 ,
,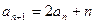 ,记
,记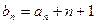 ,
, .
.
(Ⅰ)证明:数列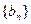 是等比数列;
是等比数列;
(Ⅱ)记 ,数列
,数列 的前n项和为
的前n项和为 ,求证:
,求证: .
.
((本小题满分12分)
如图,已知正三棱柱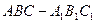 的所有棱长都为4,
的所有棱长都为4,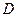 为
为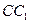 的中点.
的中点.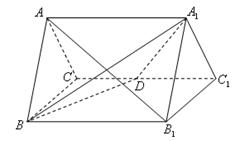
(Ⅰ)求证: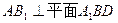 ;
;
(Ⅱ)求二面角 的大小.
的大小.
(本小题满分12分)
甲、乙两个奥运会举办城市之间有7条网线并联,这7条网线能通过的信息量分别为1,1,2,2,2,3,3(信息流量单位),现从中任选三条网线,设可通过的信息量为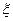 . 若可通过的信息量
. 若可通过的信息量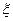 ≥6,则可保证信息通畅.
≥6,则可保证信息通畅.
(I)求线路信息通畅的概率;
(II)求线路可通过的信息量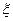 的分布列和数学期望.
的分布列和数学期望.
在 .
.
(I)求边 的长;
的长;
(II)若点 是
是 的中点,求中线
的中点,求中线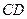 的长度.
的长度.
已知函数f(x)是定义在R上的偶函数,当x
 0时,f(x)=
0时,f(x)=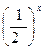 .
.
(1)画出函数f(x)的图象.
(2)根据图象写出 f(x)的单调区间,并写出函数的值域。
f(x)的单调区间,并写出函数的值域。