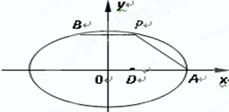
如图,在平面直角坐标系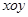 中,点
中,点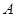 为椭圆
为椭圆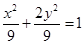 的右顶点, 点
的右顶点, 点 ,点
,点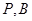 在椭圆上,
在椭圆上,  .
.
(1)求直线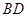 的方程;
的方程;
(2)求直线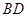 被过
被过 三点的圆
三点的圆 截得的弦长;
截得的弦长;
已知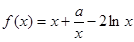 ,
,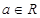
(1)讨论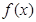 的单调区间;
的单调区间;
(2)若对任意的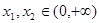 ,且
,且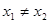 ,有
,有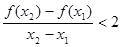 ,求实数
,求实数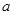 的取值范围.
的取值范围.
哈尔滨市五一期间决定在省妇女儿中心举行中学生“蓝天绿树、爱护环境”围棋比赛,规定如下:
两名选手比赛时每局胜者得1分,负者得0分,比赛进行到有一人比对方多3分或打满7局时停止.
设某学校选手甲和选手乙比赛时,甲在每局中获胜的概率为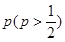 ,且各局胜负相互独立.已知
,且各局胜负相互独立.已知
第三局比赛结束时比赛停止的概率为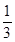 .
.
(1)求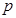 的值;
的值;
(2)求甲赢得比赛的概率;
(3)设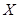 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量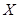 的分布列和数学期望.
的分布列和数学期望.
已知函数 ,
,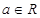
(1)讨论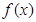 单调区间;
单调区间;
(2)当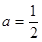 时,证明:当
时,证明:当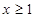 时,证明:
时,证明: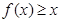 。
。
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下 联表:
联表:
| 优秀 |
非优秀 |
合计 |
|
| 甲班 |
30 |
||
| 乙班 |
50 |
||
| 合计 |
200 |
已知全部200人中随机抽取1人为优秀的概率为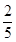
(1)请完成上面 联表;
联表;
(2)根据列联表的数据,能否有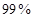 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”
(3)从全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为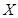 ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求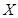 的分布列,期望
的分布列,期望 和方差
和方差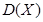
参考公式与参考数据如下:
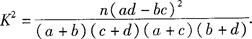
已知函数 ,
, ,若函数
,若函数 在
在 处的切线方程为
处的切线方程为 ,
,
(1)求 的值;
的值;
(2)求函数 的单调区间。
的单调区间。