某商店经销一种奥运会纪念品，每件产品的成本为30元，并且每卖出一件产品需向税务部门上交
元（为常数，2≤a≤5 ）的税收。设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与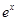
(e为自然对数的底数)成反比例。已知每件产品的日售价为40元时，日销售量为10件。
(1)求该商店的日利润L（x）元与每件产品的日售价x元的函数关系式；
(2)当每件产品的日售价为多少元时，该商品的日利润L（x）最大，并求出L（x）的最大值。
.已知直线
的参数方程是
（t是参数）圆C的极坐标方程为
.
(1)求圆C在直角坐标系下的方程；
(2)由直线上的点向圆引切线，求切线长的最小值.
A 为圆外一点，AB,AC分别交圆于D, E, AB, AC的长分别是一元二次方程x2-x+(m2 –m + 
)=0
的两个根.( 如图所示)（1）求m的值（2）求证：DE//BC
已知函数f(x)= xlnx.
(1) 求函数f(x)的单调区间和最小值；
(2)当b>0时，求证：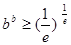
(其中e为自然对数的底数);
(3)若a>0,b>0, 求证：f(a)+(a+
b)ln2 ³ f(a+b)- f(b).
如图所示，椭圆C：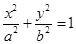
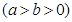的一个焦点为F(1,0)，且过点(2,0)
(1)求椭圆C的方程;
(2)已知A、B为椭圆上的点，且直线AB垂直于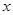
轴，又直线
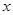：＝4与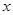轴交于点N，直线AF与BN交
于点M.
(ⅰ)求证：点M恒在椭圆C上；
(ⅱ)求△AMN面积的最大值．
如图示,四棱锥P----ABCD的底面是边长为1的正方形，PA^CD，PA = 1， PD =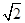 
,E为PD上一点，PE = 2ED.
(1)求证：PA ^平面ABCD；
(2)求二面角D---AC---E的正切值；
(3)在侧棱PC上是否存在一点F，使得BF // 平面AEC？若存在，指出F点的位置，并证明；若不存在，
说明理由.