某电厂冷却塔的外形是如图所示的双曲线的一部分，绕其中轴(即双曲线的虚轴)旋转所成的曲面，其中A、A′是双曲线的顶点，C、C′是冷却塔上口直径的两个端点，B、B′是下底直径的两个端点，已知AA′="14" m，CC′="18" m,BB′="22" m,塔高20 m.建立坐标系并写出该双曲线方程.
定义在[﹣1，1]上的奇函数f（x）满足f（1）=2，且当a，b∈[﹣1，1]，a+b≠0时，有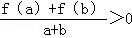
．
（1）试问函数f（x）的图象上是否存在两个不同的点A，B，使直线AB恰好与y轴垂直，若存在，求出A，B两点的坐标；若不存在，请说明理由并加以证明．
（2）若
对所有x∈[﹣1，1]，a∈[﹣1，1]恒成立，求实数m的取值范围．
设函数
的定义域为E，值域为F．
（1）若E={1，2}，判断实数λ=lg22+lg2lg5+lg5﹣
与集合F的关系；
（2）若E={1，2，a}，F={0，
}，求实数a的值．
（3）若
，F=[2﹣3m，2﹣3n]，求m，n的值．
已知关于x的方程：x2﹣（6+i）x+9+ai=0（a∈R）有实数根b．
（1）求实数a，b的值．
（2）若复数z满足|
﹣a﹣bi|﹣2|z|=0，求z为何值时，|z|有最小值，并求出|z|的值．
已知函数
，
．
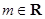（1）若
，求证：函数
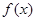是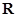
上的奇函数；
（2）若函数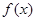在区间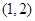
上没有零点，求实数
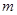的取值范围．
已知命题
，命题
。
（1）若p是q的充分条件，求实数m的取值范围；
（2）若m=5，“
”为真命题，“
”为假命题，求实数x的取值范围。