(本小题满分12分)有A、B、C、D、E五位工人参加技能竞赛培训.现分别从A、B二人在培训期间参加的若干次预赛成绩中随机抽取8次.用茎叶图表示这两组数据如下:
(Ⅰ) 现要从A、B中选派一人参加技能竞赛,从平均状况和方差的角度考虑,你认为派哪位工人参加合适?请说明理由;
(Ⅱ) 若从参加培训的5位工人中选2人参加技能竞赛,求A、B二人中至少有一人参加技能竞赛的概率.
已知函数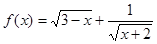 的定义域为集合
的定义域为集合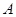 ,
,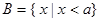 .
.
(1)若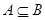 ,求实数a的取值范围;
,求实数a的取值范围;
(2)若全集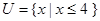 ,a=
,a=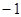 ,求
,求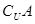 及
及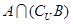 .
.
(本题12分)如图,在侧棱锥垂直底面的四棱锥ABCD-A1B1C1D1中,AD∥BC,
AD⊥AB,AB= 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
与直线AA1的交点。
(1)证明:(i)EF∥A1D1;
(ii)BA1⊥平面B1C1EF;
(2)求BC1与平面B1C1EF所成的角的正弦值。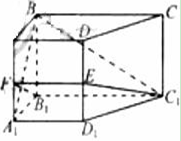
(本题8分)如图,ABCD是正方形,O是正方形的中心, PO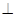 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE(2)平面PAC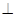 平面BDE
平面BDE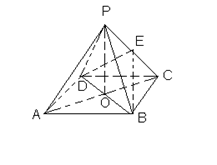
(本题6分)已知圆台的母线长为4 cm,母线与轴的夹角为30°,上底面半径是下底面半径的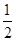 ,求这个圆台的侧面积.
,求这个圆台的侧面积.
(本题6分)已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S。