(本小题满分12分)如图,在△ABC中,|AB|=|AC|= ,|BC|=2,以B、C为焦点的椭圆恰好过AC的中点P.
,|BC|=2,以B、C为焦点的椭圆恰好过AC的中点P.
(Ⅰ)求椭圆的标准方程;
(Ⅱ) 过椭圆的右顶点作直线l与圆E:(x-1)2+y2=2相交于M、N两点,试探究点M、N能将圆E分割成弧长比值为1∶3的两段弧吗?若能,求出直线l的方程;若不能,请说明理由.
(本小题12分)在△ABC中,内角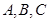 的对边分别为
的对边分别为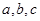 ,且
,且
(Ⅰ)求角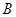 的大小;
的大小;
(II)若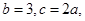 求
求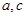 的值.
的值.
(本小题12分)如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
(Ⅰ)求证:DM∥平面APC;
(II)求证:平面ABC⊥平面APC.
(本小题满分14分)
已知函数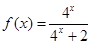 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若数列
 ,
,
求数列 的通项公式;
的通项公式;
(Ⅲ)若数列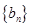 满足
满足 ,
, 是数列
是数列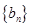 的前
的前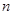 项和,是否存在正实数
项和,是否存在正实数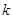 ,使不等式
,使不等式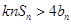 对于一切的
对于一切的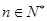 恒成立?若存在,请求出
恒成立?若存在,请求出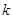 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分12分)
已知点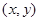 是区域
是区域 ,(
,(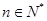 )内的点,目标函数
)内的点,目标函数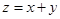 ,
, 的最大值记作
的最大值记作 .若数列
.若数列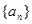 的前
的前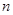 项和为
项和为 ,
, ,且点(
,且点( )在直线
)在直线 上.
上.
(Ⅰ)证明:数列 为等比数列;
为等比数列;
(Ⅱ)求数列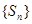 的前
的前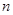 项和
项和 .
.
(本小题满分12分)
攀岩运动是一项刺激而危险的运动,如图(1)在某次攀岩活动中,两名运动员在如图所在位置,为确保运动员的安全,地面救援者应时刻注意两人离地面的距离,以备发生危险时进行及时救援. 为了方便测量和计算,画出示意图,如图(2)所示,点 分别为两名攀岩者所在位置,点
分别为两名攀岩者所在位置,点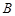 为山的拐角处,且斜坡AB的坡角为
为山的拐角处,且斜坡AB的坡角为 ,点
,点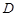 为山脚,某人在地面上的点
为山脚,某人在地面上的点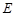 处测得
处测得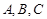 的仰角分别为
的仰角分别为 ,
, 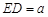 ,
,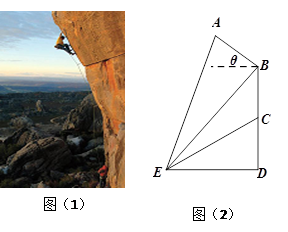
求:(Ⅰ)点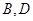 间的距离及点
间的距离及点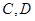 间的距离;
间的距离;
(Ⅱ)在点 处攀岩者距地面的距离
处攀岩者距地面的距离 .
.