已知函数 .
.
(Ⅰ)当 时,求证:函数
时,求证:函数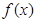 在
在 上单调递增;
上单调递增;
(Ⅱ)若函数 有三个零点,求
有三个零点,求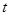 的值.
的值.
(本小题满分13分)如图,在四棱锥中,底面是正方形,底面,, 点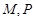 分别是
分别是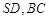 的中点,,且交于点.
的中点,,且交于点.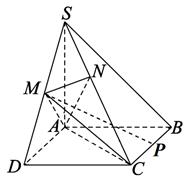
(Ⅰ)求证: 平面
平面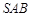 ;
;
(Ⅱ)求证:平面⊥平面;
(Ⅲ)求二面角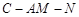 的余弦值.
的余弦值.
已知
(Ⅰ)求函数的最小正周期和对称中心;
(Ⅱ)将函数的图象向右平移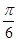 个单位,得到函数
个单位,得到函数 的图象,当时,方程
的图象,当时,方程 有实数解,求实数的取值范围.
有实数解,求实数的取值范围.
关于 的不等式
的不等式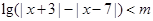 .
.
(Ⅰ)当 时,解此不等式;
时,解此不等式;
(Ⅱ)设函数 ,当
,当 为何值时,
为何值时, 恒成立?
恒成立?
已知曲线 的极坐标方程是
的极坐标方程是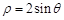 ,直线
,直线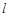 的参数方程是
的参数方程是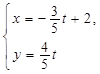 (
(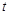 为参数).
为参数).
(Ⅰ)将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)设直线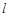 与
与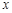 轴的交点是
轴的交点是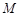 ,
, 是曲线
是曲线 上一动点,求
上一动点,求 的最大值.
的最大值.
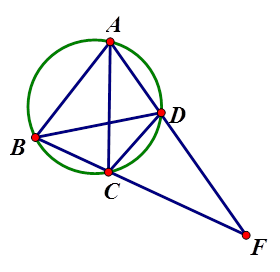
已知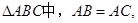
 外接圆劣弧
外接圆劣弧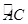 上的点(不与点
上的点(不与点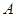 、
、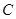 重合),延长
重合),延长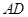 交
交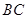 的延长线于
的延长线于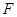 .
.
(Ⅰ)求证: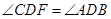 ;
;
(Ⅱ)求证: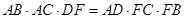 .
.