1、证明两角差的余弦公式 ;
;
2、由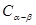 推导两角和的余弦公式
推导两角和的余弦公式 .
.
3、已知△ABC的面积 ,且
,且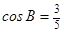 ,求
,求 .
.
已知全集U={1,2,3,4,5,6,7,8},M ={1,3,5,7},N ={5,6,7},则Cu( M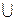 N)=()
N)=()
A.{5,7 } } |
B.{2,4} | C.{2,4,8} | D.{1,3,5,6,7} |
在直角坐标平面上有一点列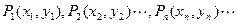 ,对一切正整数
,对一切正整数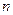 ,点
,点 位于函数
位于函数 的图象上,且
的图象上,且 的横坐标构成以
的横坐标构成以 为首项,
为首项, 为公差的等差数列
为公差的等差数列 。
。
⑴求点 的坐标;
的坐标;
⑵设抛物线列 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于 轴,第
轴,第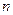 条抛物线
条抛物线 的顶点为
的顶点为 ,且过点
,且过点 ,记与数列
,记与数列 相切于
相切于 的直线的斜率为
的直线的斜率为 ,求:
,求: 。
。
⑶设 ,等差数列
,等差数列 的任一项
的任一项 ,其中
,其中 是
是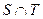 中的最大数,
中的最大数, ,求
,求 的通项公式。
的通项公式。
(本小题12分)如图,四面体ABCD中,O、E分别是BD、BC的中点,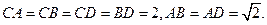
(I)求证: 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。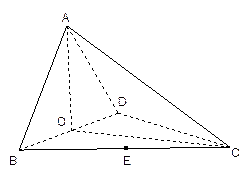
(本小题满分14分)
已知数列 满足
满足 ,
,
 是实数).
是实数).
(1)若 ,
,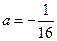 ,求通项
,求通项 ;
;
(2)若 ,设数列
,设数列 的前
的前 项和当
项和当 时为
时为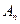 ,当
,当 时为
时为 ,
,
求证:
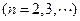 .
.
(本小题满分12分)
如图,以原点O为顶点,以y轴为对称轴的抛物线E的焦点为F(0,1),点M是直线 上任意一点,过点M引抛物线E的两条切线分别交x轴于点S , T,切点分别为B、A。
上任意一点,过点M引抛物线E的两条切线分别交x轴于点S , T,切点分别为B、A。
(1)求抛物线E的方程;
(2)求证:点S,T在以FM为直径的圆上;
(3)当点M在直线 上移动时,直线AB恒过焦点F,求
上移动时,直线AB恒过焦点F,求 的值。
的值。