在直角坐标平面上有一点列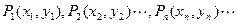 ,对一切正整数
,对一切正整数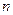 ,点
,点 位于函数
位于函数 的图象上,且
的图象上,且 的横坐标构成以
的横坐标构成以 为首项,
为首项, 为公差的等差数列
为公差的等差数列 。
。
⑴求点 的坐标;
的坐标;
⑵设抛物线列 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于 轴,第
轴,第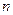 条抛物线
条抛物线 的顶点为
的顶点为 ,且过点
,且过点 ,记与数列
,记与数列 相切于
相切于 的直线的斜率为
的直线的斜率为 ,求:
,求: 。
。
⑶设 ,等差数列
,等差数列 的任一项
的任一项 ,其中
,其中 是
是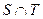 中的最大数,
中的最大数, ,求
,求 的通项公式。
的通项公式。
在 中,已知角
中,已知角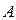 ,
,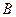 ,
,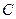 的对边分别是
的对边分别是 ,
, ,
, ,且
,且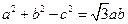 .
.
(1)求角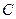 的大小;
的大小;
(2)如果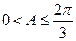 ,
, ,求实数
,求实数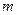 的取值范围.
的取值范围.
航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km/h.飞机先看到山顶的俯角为150,经过420s后又看到山顶的俯角为450,求山顶的海拔高度(取 =1.4,
=1.4, =1.7).
=1.7).
在 中,已知
中,已知 ,
, .
.
(1)若 ,求
,求 ;
;
(2)求 的最大角的弧度数.
的最大角的弧度数.
在 中,
中, 分别是角
分别是角 ,
, ,
, 所对边的长,
所对边的长, 是
是 的面积.已知
的面积.已知 ,求
,求 的值.
的值.
如图,海中有一小岛,周围 海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变航行的方向继续前进,问此舰有没有触礁的危险
海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变航行的方向继续前进,问此舰有没有触礁的危险