如图,BA是⊙O的直径,AD是切线,BF、BD是割线,求证:BE•BF=BC•BD.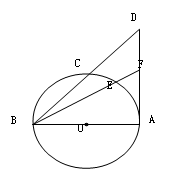
如图所示,在正方体ABCD—A1B1C1D1中,棱长为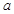 ,E为棱CC1上的动点.
,E为棱CC1上的动点.
⑴求证:A1E⊥BD;
⑵当E恰为棱CC1的中点时,求二面角A1—BD—E的大小;
⑶在⑵的条件下,求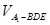 。
。
已知圆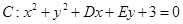 关于直线
关于直线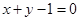 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为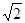 。
。
⑴求圆C的方程;
⑵已知不过原点的直线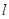 与圆C相切,且
与圆C相切,且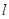 在
在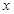 轴、
轴、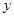 轴上的截距相等,求直线
轴上的截距相等,求直线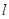 的方程。
的方程。
已知动点P到两定点 距离之比为
距离之比为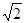 。
。
⑴求动点P轨迹C的方程;
⑵若过点N的直线 被曲线C截得的弦长为
被曲线C截得的弦长为 ,求直线
,求直线 的方程。
的方程。
已知直线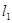 经过点A
经过点A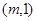 ,B
,B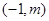 ,直线
,直线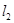 经过点P
经过点P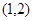 ,Q
,Q 。
。
⑴若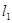 //
//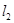 ,求
,求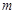 的值;
的值;
⑵若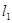 ⊥
⊥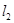 ,求
,求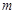 的值。
的值。
如图,在长方体ABCD—A1B1C1D1中,AA1=AD=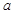 ,AB=2
,AB=2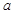 ,E,F分别为C1D1,
,E,F分别为C1D1,
A1D1的中点。
⑴求证:DE/⊥平面BCE;
⑵求证:AF//平面BDE。