已知圆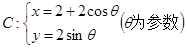
，直线l:
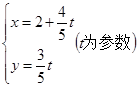
（1）求圆C的普通方程.若以原点为极点，以x轴的正半轴为极轴建立极坐标系，写出圆C的极坐标方程.
（2）判断直线l与圆C的位置关系，并说明理由；若相交，请求出弦长
为预防
病毒暴发，某生物技术公司研制出一种新流感疫苗，为测试该疫苗的有效性（若疫苗有效的概率小于90%，则认为测试没
有通过），公司选定2000个流感样本分成三组，测试结果如下表：
| A组 |
B组 |
C组 |
|
| 疫苗有效 |
673 |
 |
 |
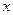| 疫苗无效 |
77 |
90 |
 |
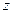已知在全体样本中随机抽取1个，抽到B组疫苗有效的概率是0．33．
（1）求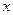的值；
（2）现用分层抽样的方法在全体样本中抽取360个测试结果，问应在C组抽取多少个？
（3）已知
,求不能通过测试的概率．
已知向量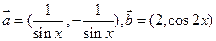
，其中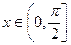
．
（1）试判断向量
与
能否平行，并说明理由？
（2）求函数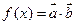
的最小值．
（本小题满分12分）
设函数
（Ⅰ）若函
数
在其定义域内是增函数，求
的取值范围；
（Ⅱ）设
，方程
有两根
，记
.试探究
值的符号，其中
是
的导函数.
（本小题满分12分）
已知点
和直线
，作
垂足为Q，且
（Ⅰ）求点P的轨迹方程;
（Ⅱ）过点C的直线
与点P轨迹交于两点
，
，点
，若
的面积为
，求直线的方程.
（本小题满分12分）
设数列
为等差数列，且
，
，数列
的前
项和为
，
且
；，
（Ⅰ）求数列,的通项公式；
（Ⅱ）若
，
为数列
的前项和. 求证：
.