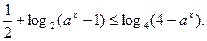（本小题满分12分）
已知点
和直线
，作
垂足为Q，且
（Ⅰ）求点P的轨迹方程;
（Ⅱ）过点C的直线
与点P轨迹交于两点
，
，点
，若
的面积为
，求直线的方程.
设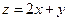
，式中变量
满足条件
，求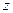
的最大值和最小值.
已知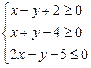
，求：（1）
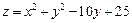的最小值;（2）
的范围．
.某人上午7时，乘摩托艇以匀速
海里/时(4≤≤20)从
港出发到距50海里的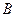
港去，然后乘汽车以
千米/时(30≤≤100)自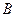港向距300千米的
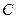市驶去，应该在同一天下午4至9点到达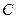市.设汽车、摩托艇所需的时间分别是
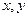小时.
(1)写出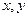所满足的条件，并在所给的平面直角坐标系内，作出表示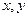范围的图形；
(2)如果已知所需的经费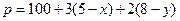
(元)，那么
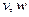分别是多少时走得最经济？此时需花费多少元？
已知二次函数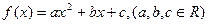
满足：对任意实数x，都有
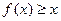，且当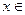
（1，3）时，有
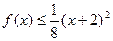成立。
（1）证明：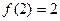
;
（2）若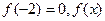
的表达式;
（3）设
,
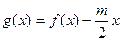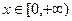，若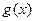
图上的点都位于直线
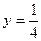的上方，求
实数m的取值范围。
已知ａ＞０，且ａ≠１，解关于x的不等式：