.某人上午7时,乘摩托艇以匀速 海里/时(4≤
海里/时(4≤ ≤20)从
≤20)从 港出发到距50海里的
港出发到距50海里的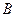 港去,然后乘汽车以
港去,然后乘汽车以 千米/时(30≤
千米/时(30≤ ≤100)自
≤100)自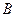 港向距300千米的
港向距300千米的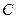 市驶去,应该在同一天下午4至9点到达
市驶去,应该在同一天下午4至9点到达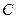 市.设汽车、摩托艇所需的时间分别是
市.设汽车、摩托艇所需的时间分别是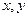 小时.
小时.
(1)写出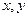 所满足的条件,并在所给的平面直角坐标系内,作出表示
所满足的条件,并在所给的平面直角坐标系内,作出表示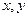 范围的图形;
范围的图形;
(2)如果已知所需的经费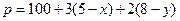 (元),那么
(元),那么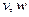 分别是多少时走得最经济?此时需花费多少元?
分别是多少时走得最经济?此时需花费多少元?
某校从参加高一年级期中考试的学生中随机抽取 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段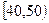 ,
, …
…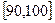 后得到如下部分频率分布直方图.(见下一页图)观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.(见下一页图)观察图形的信息,回答下列问题:
(Ⅰ)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ)用分层抽样的方法在分数段为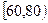 的学生中抽取一个容量为
的学生中抽取一个容量为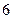 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取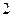 人,求至多有
人,求至多有 人在分数段
人在分数段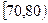 的概率。
的概率。

已知{an}是正数组成的数列,a1=1,且点( )(n
)(n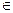 N*)在函数y=x2+1的图象上。 (Ⅰ)求数列{an}的通项公式;
N*)在函数y=x2+1的图象上。 (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足bn= (n∈N*),求数列{bn}的前n项和
(n∈N*),求数列{bn}的前n项和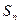 。
。
已知向量 ,函数
,函数 的图像上一个最高点的坐标为
的图像上一个最高点的坐标为 ,与之相邻的一个最低点的坐标
,与之相邻的一个最低点的坐标 .
.
(1)求 的解析式.
的解析式.
(2)在△ 中,
中, 是角
是角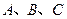 所对的边,且满足
所对的边,且满足 ,求角
,求角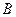 的大小以及
的大小以及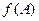 取值范围.
取值范围.
(本小题12分)如图,在长方体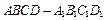 中,点
中,点 在棱
在棱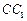 的延长线上,且
的延长线上,且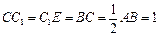 .下标
.下标
(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面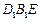
 平面
平面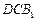 ;
;
(3)求四面体 的体积.
的体积.
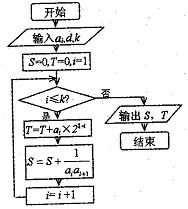
如图所示,流程图给出了无穷等差整数列 ,
, 时,输出的
时,输出的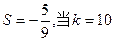 时,输出的
时,输出的 (其中d为公差)
(其中d为公差)
(I)求数列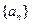 的通项公式
的通项公式
(II)是否存在最小的正数m,使得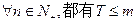 成立?若存在,求出m的值,若不存在,请说明理由。
成立?若存在,求出m的值,若不存在,请说明理由。