如图所示,流程图给出了无穷等差整数列 ,
, 时,输出的
时,输出的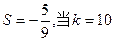 时,输出的
时,输出的 (其中d为公差)
(其中d为公差)
(I)求数列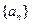 的通项公式
的通项公式
(II)是否存在最小的正数m,使得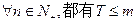 成立?若存在,求出m的值,若不存在,请说明理由。
成立?若存在,求出m的值,若不存在,请说明理由。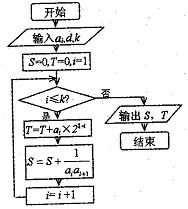
(本小题满分12分)已知等差数列 的前
的前 项和为
项和为 ,公差d
,公差d 0,
0, ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和公式.
项和公式.
(本小题满分12分)如图4平面四边形ABCD中,AB=AD= ,BC=CD=BD,设
,BC=CD=BD,设 .
.
(1)将四边形ABCD的面积S表示为 的函数;
的函数;
(2)求四边形ABCD面积S的最大值及此时 值.
值.
(本小题满分12分)已知函数
 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)当 时,求函数
时,求函数 的取值范围.
的取值范围.
(12分)我们把同时满足下列两个性质的函数称为“和谐函数” :
①函数在整个定义域上是单调增函数或单调减函数;
②在函数的定义域内存在区间 ,使得函数在区间
,使得函数在区间 上的值域为
上的值域为 .
.
⑴已知幂函数 的图像经过点
的图像经过点 ,判断
,判断
 是否是和谐函数?
是否是和谐函数?
⑵判断函数 是否是和谐函数?
是否是和谐函数?
⑶若函数 是和谐函数,求实数
是和谐函数,求实数 的取值范围.
的取值范围.
(12分)已知定义域为 的偶函数
的偶函数 .
.
(1)求实数 的值;
的值;
(2)判断并证明 的单调性;
的单调性;
(3)若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.