2013年4月14日,CCTV财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象.为了研究使用淡化海砂与混凝土耐久性是否达标有关,某大学实验室随机抽取了60个样本,得到了相关数据如下表:
| |
混凝土耐久性达标 |
混凝土耐久性不达标 |
总计 |
| 使用淡化海砂 |
25 |
 |
30 |
| 使用未经淡化海砂 |
 |
15 |
30 |
| 总计 |
40 |
20 |
60 |
(Ⅰ)根据表中数据,求出 ,
, 的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?
的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?
(Ⅱ)若用分层抽样的方法在使用淡化海砂的样本中抽取了6个,现从这6个样本中任取2个,则取出的2个样本混凝土耐久性都达标的概率是多少?
参考数据:
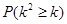 |
0.10 |
0.050 |
0.025 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
参考公式: 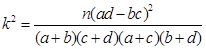
某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试(满分150分),若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
(1)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(2)若通过学校选拔测试的学生将代表学校参加市知识竞赛,知识竞赛分为初赛和复赛,初赛中每人最多有5次答题机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛.假设参赛者甲答对每一个题的概率都是 ,求甲在初赛中答题个数的分布列和数学期望.
,求甲在初赛中答题个数的分布列和数学期望.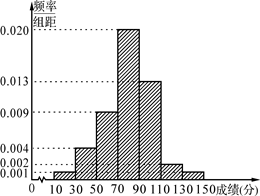
已知数列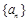 的前n项和为
的前n项和为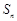 满足:
满足: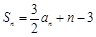 .
.
(1)求证:数列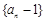 是等比数列;
是等比数列;
(2)令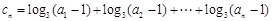 ,对任意
,对任意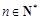 ,是否存在正整数m,使
,是否存在正整数m,使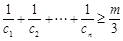 都成立?若存在,求出m的值;若不存在,请说明理由.
都成立?若存在,求出m的值;若不存在,请说明理由.
设平面向量 ,
,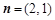 ,函数
,函数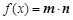 .
.
(1)当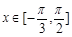 时,求函数
时,求函数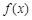 的取值范围;
的取值范围;
(2)当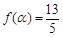 ,且
,且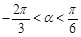 时,求
时,求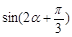 的值.
的值.
已知函数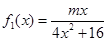 ,
,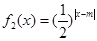 ,其中m∈R.
,其中m∈R.
(1)若0<m≤2,试判断函数f (x)=f1 (x)+f2 (x) 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(2)设函数 若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.
若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) =" g" (x2) 成立,试确定实数m的取值范围.
已知数列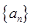 ,
, 满足
满足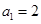 ,
,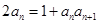 ,
,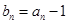 ,数列
,数列 的前
的前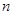 项和为
项和为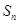 ,
,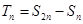 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求证: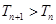 ;
;
(3)求证:当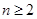 时,
时,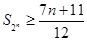 .
.