设函数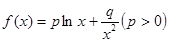 ,若
,若 时,
时, 有极小值
有极小值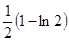 ,
,
(1)求实数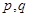 的取值;
的取值;
(2)若数列 中,
中,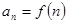 ,求证:数列
,求证:数列 的前
的前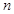 项和
项和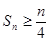 ;
;
(3)设函数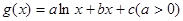 ,若
,若 有极值且极值为
有极值且极值为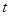 ,则
,则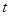 与
与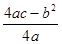 是否具有确定的大小关系?证明你的结论.
是否具有确定的大小关系?证明你的结论.
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.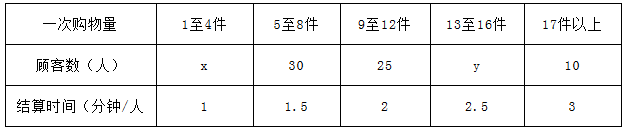
已知这100位顾客中一次购物量超过8件的顾客占55%.
(1)确定x,y的值,并求顾客一次购物的结算时间的平均值;
(2)求一位顾客一次购物的结算时间不超过2 min的概率.
(注:将频率视为概率)
已知 :
: ,
, :
: ,若
,若 是
是 的必要不充分条件,求实数m的取值范围.
的必要不充分条件,求实数m的取值范围.
(1)试用辗转相除法求840与1 764的最大公约数.
(2)利用秦九韶算法求多项式f(x)=2x5+4x4-2x3+8x2+7x+4当x=3的值,写出每一步的计算表达式.
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为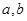 .
.
(Ⅰ)求直线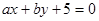 与圆
与圆 相切的概率;
相切的概率;
(Ⅱ)将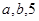 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
设关于 的一元二次方程
的一元二次方程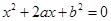
(Ⅰ)若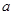 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,
是从0,1,2三个数中任取的一个数,
求上述方程有实数根的概率;
(Ⅱ)若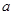 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实数根的概率.
任取的一个数,求上述方程有实数根的概率.