设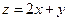 ,式中变量
,式中变量 满足条件
满足条件 ,求
,求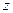 的最大值和最小值.
的最大值和最小值.
某校从高中部年满16周岁的学生中随机抽取来自高二和高三学生各10名,测量他们的身高,数据如下(单位:cm)
高二:166,158,170,169,180,171,176,175,162,163
高三:157,183,166,179,173,169,163,171,175,178
(1)若将样本频率视为总体的概率,从样本中来自高二且身高不低于170的学生中随机抽取3名同学,求其中恰有两名同学的身高低于175的概率;
(2)根据抽测结果补充完整下列茎叶图,并根据茎叶图对来自高二和高三学生的身高作比较,写出两个统计结论.
已知函数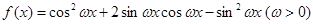 ,且周期为
,且周期为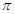 .
.
(1)求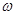 的值;
的值;
(2)当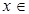 [
[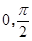 ]时,求
]时,求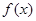 的最大值及取得最大值时
的最大值及取得最大值时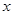 的值.
的值.
已知函数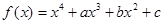 ,在
,在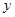 轴上的截距为
轴上的截距为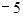 ,在区间
,在区间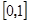 上单调递增,在
上单调递增,在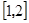 上单调递减,又当
上单调递减,又当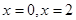 时取得极小值.
时取得极小值.
(1)求函数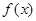 的解析式;
的解析式;
(2)能否找到函数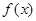 垂直于
垂直于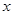 轴的对称轴,并证明你的结论;
轴的对称轴,并证明你的结论;
(3)设使关于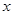 的方程
的方程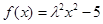 恰有三个不同实根的实数
恰有三个不同实根的实数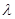 的取值范围为集合
的取值范围为集合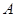 ,且两个非零实根为
,且两个非零实根为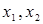 ,试问:是否存在实数
,试问:是否存在实数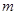 ,使得不等式
,使得不等式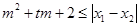 对任意
对任意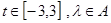 恒成立?若存在,求
恒成立?若存在,求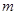 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知点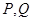 的坐标分别为
的坐标分别为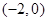 ,
,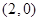 ,直线
,直线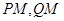 相交于点
相交于点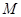 ,且它们的斜率之积是
,且它们的斜率之积是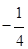
(1)求点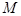 的轨迹方程;
的轨迹方程;
(2)过点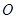 作两条互相垂直的射线,与点
作两条互相垂直的射线,与点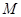 的轨迹交于
的轨迹交于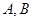 两点.试判断点
两点.试判断点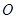 到直线
到直线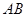 的距离是否为定值.若是请求出这个定值,若不是请说明理由.
的距离是否为定值.若是请求出这个定值,若不是请说明理由.
已知数列 的前
的前 项和为
项和为 ,向量
,向量 ,
, ,满足条件
,满足条件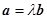 ,
, 且
且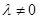 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设函数 ,数列
,数列 满足条件
满足条件 ,
,
①求数列 的通项公式;
的通项公式;
②设 ,求数列
,求数列 的前
的前 和
和 .
.